The Fractal Dimension “D” is a measure of how completely a Fractal appears to fill space as one zooms down to finer and finer scales. So what is a fractal? It is a rough or fragmented shape that can be split into parts, each of which is at least similar to a reduced size copy of the original. The following video illustrates the beauty of fractals in 3D and is well worth watching in full screen:
.
AMAZING – 3D Evolving Fractal Landscape
.
.
Below is an example of a fractal called the Koch Curve:
.
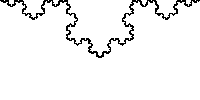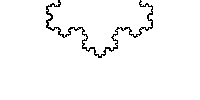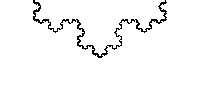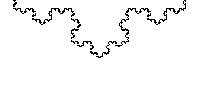 Notice how no matter what scale you view the Koch Curve in it looks very similar? This characteristic is called self similarity and defines a fractal shape. Can you see anything strange about the chart below?
Notice how no matter what scale you view the Koch Curve in it looks very similar? This characteristic is called self similarity and defines a fractal shape. Can you see anything strange about the chart below?
.
 .
.
Without being told would you have known that the left half of the chart above was 5 years of monthly bars and the right half was 15 days on 30 minute bars? Probably not, because price movements look similar no matter what time frame we are viewing them in, this is self similarity and why the financial markets are considered fractals.
The Wiener process is also a fractal and looks very much like stock price movements. It is a continuous time stochastic process that charts Brownian Motion and is used in the mathematical theory of finance as well as the Black-Scholes option pricing model. It is clearly self similar and the average features of the function do not change while zooming in. Image by Cyp:
.
.
Usually we think of things in whole, rather than partial dimensions and at first I found this a foreign concept, but try thinking of it this way: A shape like a stock chart is too big to be one dimensional but too thin to be two dimensional, so its Fractal Dimension results in a reading between 1 and 2.
It is easy to understand the number of dimensions in a line, square or cube. A line has 1 dimension – length, a square has 2 – length and width and a cube has 3 – length, width and depth. However if we use this very simplistic thought process to try and reveal the Dimension of a fractal like the Sierpinski triangle then we run into problems.

It is clear that we need a more intelligent approach for identifying the dimension of self similar shapes so lets look at it in another way: If we break a line segment into 4 self similar parts of the same length, a magnification factor of 4 is needed to reveal the original shape. If we break a line segment into 7 self similar parts, a magnification factor of 7 will yield the original shape… 20 parts, magnification of 20 etc. Therefore we can break a line segment into “N” self similar parts and a magnification factor of “N” will reveal the original shape.
If we break a square into four self similar sub squares then a magnification factor of 2 is needed to reveal the original shape. 9 self similar parts will require a magnification factor of 3 and 25 self similar parts will require a magnification factor of 5. As a result we can conclude that a square can be broken into N^2 self similar copies and to reveal the original shape a magnification factor of “N” must be used. A cube can be broken into N^3 self similar pieces and once again the original shape is found using a magnification factor of “N”.
So a more accurate way of thinking about the Dimension of a object is to say that “D” is the exponent of the number of self similar pieces with a magnification factor of “N” which a shape can be broken into.
Using this thought process, lets look again at the dimension of the Sierpinski triangle. How do we find the exponent in this case? Now we are going to need logarithms (log).
What is Log?
Log reveals the power that a number needs to be raised to in order to produce a given result. Unless otherwise stated the base number is 10, therefore:
Log(1000) = 3
Because
10^3 = 10 * 10 * 10
10^3 = 1000
Returning to our previous conclusions – we know that for a square we have N^2 self-similar pieces, each with a magnification factor of N etc… So:

The Sierpinski triangle is made up of 3 self similar pieces that require a magnification factor of 2 to reveal the original shape. Therefore:
D = log (number of self similar pieces) / log (magnification factor)
= log 3 / log 2
= 1.58
The Sierpinski triangle also contains 27 self similar pieces that require a magnification factor of 8 to reveal the original shape so:
D = log (number of self similar pieces) / log (magnification factor)
= log 27 / log 8
= 1.58
In addition to this we know that the Sierpinski triangle breaks into 3^N self similar parts requiring a magnification factor of 2^N to reveal the original shape. Therefore:
D = log (number of self similar pieces) / log (magnification factor)
= log 3^N / log 2^N
= N * log 3 / N * log 2
= 1.58
So the Fractal Dimension is really a measure of how complicated a self similar shape is. A line is smaller and more basic than that a square, while the Sierpinski triangle sits somewhere between the two. However all three have the same number of self similar parts; they can all be divided to infinity.
****The beauty of the Fractal Dimension lies in its ability to somehow capture the notion of how large a set is.
.
Finding The Fractal Dimension of a Stock
.
John F Ehlers created a method for identifying the “D” for stocks by averaging the measured Fractal Dimension over different scales. He used this method as a component of his Fractal Adaptive Moving Average (FRAMA) and presented it again as a standalone indicator in the June 2010 edition of Technical Analysis of Stocks and Commodities – Fractal Dimension As A Market Mode Sensor.
The standard method of discovering the “D” of a shape is to cover it with a number of small objects that are various sizes and compare how many of each fit across the surface. Covering a price curve with a series of small boxes however is far too cumbersome. But because price samples are uniformly spaced (each bar is 1 day, 1 week, 10 min etc) Ehlers decided that the average slope of the curve could be used as an estimation of the box count.
This is far less complicated than it sounds as the slope is found by simply taking the highest price over a period minus the lowest price during that period and dividing the result by the number of periods. We will call this measure “HL”. We need to find the “HL” measure (slope) over the first half, second half and full length of “N” to help us find “D”.
D = (Log(HL1 + HL2) – Log(HL)) / Log(2)
Note: Log(2) = Log(N / (½N))
HL1 = (Max(High,½N..N) – Min(Low,½N..N)) / ½N
HL2 = (Max(High,½N) – Min(Low,½N)) / ½N
HL = (Max(High,N) – Min(Low,N)) / N
N = Periods
If D < 1 then D = 1
If D > 2 then D = 2
.
Finding The Fractal Dimension, Examples
.
Lets have a look at some theoretical stock prices and the resulting Fractal Dimension:
.
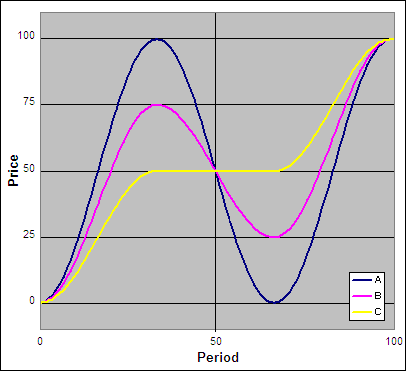
.
Above are three price curves, now lets calculate the “D” for each where “N” = 100.
D = (Log(HL1 + HL2) – Log(HL)) / Log(2)
So:

.
For ‘Curve A’ the full range is repeated in both halves of the chart so it exists fully in two Dimensions and D = 2. For ‘Curve B’ only half of the range is repeated in each half of the chart so it exists in between one and two Dimensions or specifically D = 1.58. The range for ‘Curve C’ is not repeated at all between the two halves of the chart so it exists in only one Dimension; D = 1.
.
Fractal Dimension Excel File
.
I have put together an Excel Spreadsheet that calculates the Fractal Dimension and made it available for FREE download. It contains a ‘basic’ version displaying the working and a ‘fancy’ one that will automatically adjust to the length you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Fractal Dimension (D)
.
Fractal Dimension Example
.
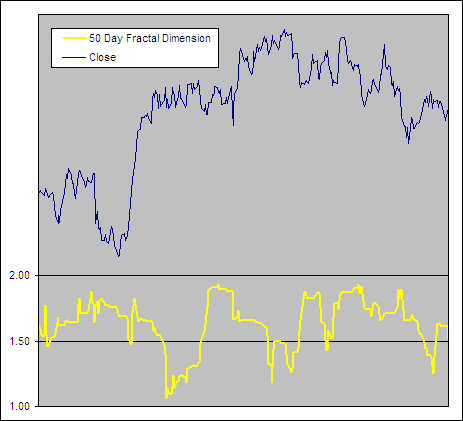
.
Uses for the Fractal Dimension
.
The lower the Fractal Dimension the closer a stock chart is to a straight line and therefore the stronger the trend. High readings on the other hand reveal a complex fractal; the shape of a range bound market. These two different market types require very different strategies in order to maximize profits and minimize losses.
Ehlers uses this measure in the FRAMA to dynamically adjust the alpha of an exponential moving average so that it reacts quickly in a trending market and slowly when prices are congested. Accurately being able to identify the strength of a trend has endless uses and therefore is worthy of much research.
.
Test Results
.
As part of the ‘Technical Indicator Fight for Supremacy‘ We have tested/will test the Fractal Dimension as a component in several technical indicators:
- Fractal Adaptive Moving Average (FRAMA) – Completed See Results
- Fractal Dimension Variable Moving Average (D-VMA) – Completed See Results
- Fractal Dimension Adaptive Moving Average (D-AMA) – Completed See Results
- Fractal Dimension Weighted Moving Average (D-WMA)
We will also test “D” as a filter taking trades only when it indicates a strong trend.
.
Further Information on Fractals
.
Woodshedder wrote thought provoking article On Fractals and Market Crashes. Here is an interesting open source platform called Fragmentarium that allows to create Fractals yourself like this:
.
.
Also here is a great documentary on Fractals:
.
Fractals – Hunting The Hidden Dimension
.

One thought on “Fractal Dimension “D””
Comments are closed.