Variable Moving Average (VMA) aka Volatility Index Dynamic Ave (VIDYA)

The Variable Moving Average (VMA) aka Volatility Index Dynamic Average (VIDYA) was developed by Tushar S. Chande and first presented in the March 1992 edition of Technical Analysis of Stocks & Commodities – Adapting Moving Averages To Market Volatility

Chande’s theory was that the performance of an exponential moving average could be improved by using a Volatility Index (VI) to adjust the smoothing period as market conditions change.  The idea being that when prices are congested an average should slow down to avoid whipsaws but when prices are trending strongly an average should speed up to capture the major price moves.

He was not the first person to think along these lines; George R. Arrington, Ph.D introduced a variable Simple Moving Average based on Standard Deviation in the June 1991 edition of Technical Analysis of Stocks & Commodities – Building a Variable-Length Moving Average (VLMA).  The YIDYA however represented a massive step forward from the VLMA because it allowed a much larger spread of smoothing periods.

.

How To Calculate a Variable Moving Average

.

VMA = (α * VI * Close) + ((1 – ( α * VI )) * VMA[1])

Where:

α = 2 / (N + 1)

VI = Users choice of a measure of volatility or trend strength.

N = User selected constant smoothing period.

Here is an example of a 3 period VMA with a 3 period Efficiency Ratio (ER) as the VI:

.

.

How the VIDYA Smoothing is changed by the Volatility Index

.

The Variable Moving Average is unique in that it has no upper or lower limit to its smoothing period:

.

.

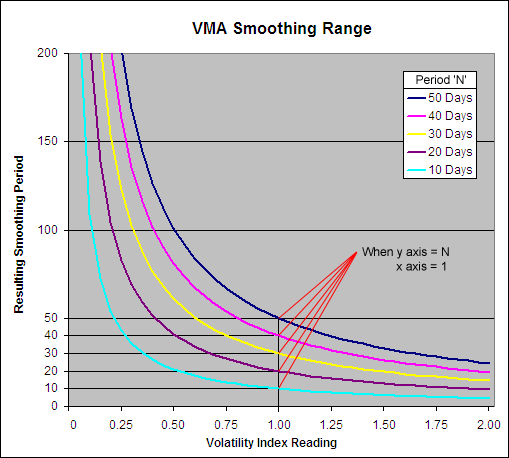
The VMA smoothing period can go infinitely high until the Volatility Index equals zero at which point the resulting average will stop moving and be equal to the previous VMA.  When the Volatility Index equals 1 the smoothing period will be equal to the user selected constant ‘N’; notice how when the Y axis = N, the X axis = 1.

However if the Volatility Index being used can rise above 1 (such as the Standard Deviation Ratio) then the smoothing period can drop below the user selected constant.  When the VI = (N/2) + 0.5 then the smoothing period will be 1, which is equal to the price itself.  Therefore the VI that is used must not rise above (N/2) + 0.5 and if it does upon occasion then this cap must be written into the formula.

.

A Look at the Actual Alpha

.

Because the VMA is as the name suggests, variable, the ‘Actual Alpha’ is not static but is influenced by the VI.  By changing the constant ‘N’ however the interpretation of the VI changes greatly:

.

.

Above you can see an example of the ‘Actual Alpha’ and the resulting smoothing period for a VMA with an ‘N’ of 1 and an ‘N’ of 5.  We know that when the VI = 1 (indicating that the stock is trending perfectly) the smoothing period = ‘N’.  So the fastest possible smoothing periods in these examples would be 1 and 5 respectively; not a big difference.  But it is surprising to see what a huge impact changing ‘N’ just a few points has overall.  In fact as ‘N’ increases the resulting VMA moves exponentially slower.  This affect is rather like the squaring used by Kaufman in his Adaptive Moving Average.

.

What Volatility Index to use?

.

Chande originally used the Standard Deviation Ratio as his VI and this is the one typically used when people talk about a VIDYA.  But later on, in the October 1995 article from Technical Analysis of Stocks & Commodities – ‘Identifying Powerful Breakouts Early‘ he suggested the use of his own Chande Momentum Oscillator (CMO).

Because the CMO ranges between 100 and -100, to use it in this application we must take the absolute value divided by 100.  The result is identical to the Efficiency Ratio (ER) and is the VI used most often when people refer to a VMA.  Any measure of volatility or trend strength can be used however as long as it fits between a zero to (N/2) + 0.5 range where higher readings indicate a stronger trend.

.

Volatility Indexes Used for Testing

.

As part of the ‘Technical Indicator Fight for Supremacy‘ we have tested/will test the following indicators as the Volatility Index in a Variable Moving Average:

• Standard Deviation Ratio (SDR) – Completed – Results
• Kaufman’s Efficiency Ratio (ER) – Completed – Results
• Relative Volatility Index (RVI) = RVI/100 – Completed – Results
• Vertical Horizontal Filter (VHF) – Completed – Results
• Fractal Dimension (D) = ABS(D – 2) – Completed – Results
• Chaikin’s Volatility (CV) * We currently lack High and Low Prices for some test markets.

Are there any others that you think are worth testing?  Please let us know in the comments section at the bottom.

.

Variable Moving Average Excel File

.

I have put together an Excel Spreadsheet containing the Variable Moving Average and made it available for FREE download.  It contains a ‘basic’ version that shows all the working and a ‘fancy’ one that will automatically adjust to the length as well as the Volatility Index you specify.  Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Variable Moving Average (VMA)

.

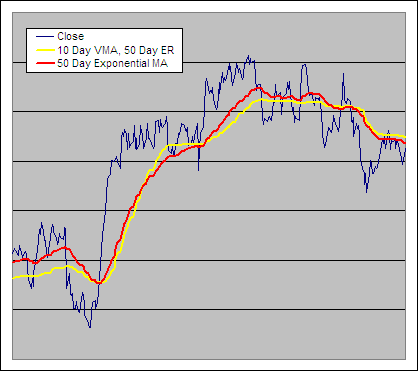
10 Day Variable Moving Average Example, VI = 50 Day Efficiency Ratio

.