Standard Deviation (SD) reveals how much a data set varies from its mean; a high Standard Deviation indicates that the data is widely spread. With stock prices it can be used as a measure of the historical volatility to reveal the theoretical probability of a price change over a specified period. This information can be used in many ways such as a measure of risk or as a component in technical indicators.
.
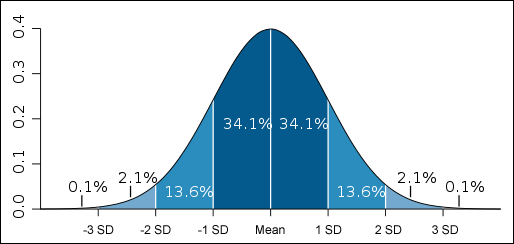
Normal Distribution Bell Curve
.
 .
.
A data set that is Normally Distributed with produce a probability curve called a bell curve, like the one above. One standard deviation from the mean accounts for 68% of the occurrences while two SDs covers 95% and three covers 99.7%. One of the challenges with the stock market is that the data is not Normally Distributed but instead exhibits Fat Tails. So the Standard Deviation is far from a perfect measure but is still a useful trading tool in some applications.
.
How To Calculate Standard Deviation
.
Standard deviation is the square root of variance and can easily be calculated in an Excel spread sheet with the =STDEVP() function or it can be done the hard way using the following formula:
.
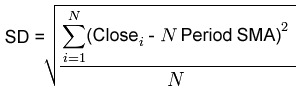
.
Where:
SMA = Simple Moving Average
N = Number of periods
.
Standard Deviation Example
.
If we take the percentage change of the Dow Jones Industrial Average for the 10 years from 2000 – 2010 we get the following values:
-6.17%, -7.1%, -16.76%, 25.32%, 3.15%, -0.61%, 16.29%, 6.43%, -33.84%, 18.82%
To find the SD we first find the mean (average):
(-6.17% + -7.1% + -16.76% + 25.32% + 3.15% + -0.61% + 16.29% + 6.43% + -33.84% + 18.82%) / N
= 5.53% / 10
= 0.55%
We then calculate the deviation of each data point from the mean (= Data Point – Mean), square the result and find the sum:
-6.72%^2 + -7.66%^2 + -17.32%^2 + 24.77%^2 + 2.6%^2 + -1.16%^2 + 15.73%^2 + 5.88%^2 + -34.39%^2 + 18.27%^2
= 28.24%
Finally divide the result by N to find the average and take the square root to reveal the SD
= √(28.24% / 10)
= 16.8%
This means that in theory (assuming a normal distribution), based on ten years of the Dow’s annual price changes, about 68% of years the Dow will move up or down within 16.8% (one standard deviation). While about 95% of years the Dow should finish up or down within 33.6% (two standard deviations).
1. A measure of the dispersion of a set of data from its mean. The more spread apart the data, the higher the deviation. Standard deviation is calculated as the square root of variance.
2. In finance, standard deviation is applied to the annual rate of return of an investment to measure the investment’s volatility. Standard deviation is also known as historical volatility and is used by investors as a gauge for the amount of expected volatility.
Investopedia explains Standard Deviation
Standard deviation is a statistical measurement that sheds light on historical volatility. For example, a volatile stock will have a high standard deviation while the deviation of a stable blue chip stock will be lower.