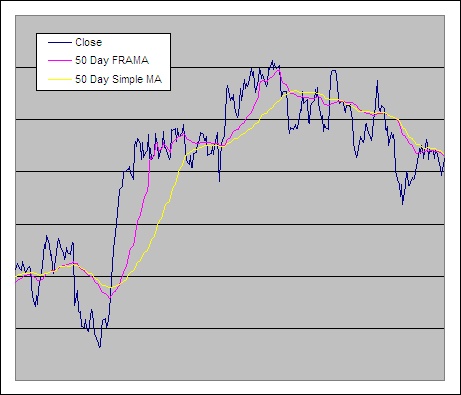
The Fractal Adaptive Moving Average aka FRAMA is a particularly clever indicator. It uses the Fractal Dimension of stock prices to dynamically adjust its smoothing period. In this post we will reveal how the FRAMA performs and if it is worthy of being included in your trading arsenal.
To fully understand how the FRAMA works please read this post before continuing. You can also download a FREE spreadsheet containing a working FRAMA that will automatically adjust to the settings you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Fractal Adaptive Moving Average (FRAMA). Please leave a comment and share this post if you find it useful.
The ‘Modified FRAMA’ that we tested consists of more than one variable. So before we can put it up against other Adaptive Moving Averages to compare their performance, we must first understand how the FRAMA behaves as its parameters are changed. From this information we can identify the best settings and use those settings when performing the comparison with other Moving Average Types.
Each FRAMA requires a setting be specified for the Fast Moving Average (FC), Slow Moving Average (SC) and the FRAMA period itself. We tested trades going Long and Short, using Daily and Weekly data, taking End Of Day (EOD) and End Of Week (EOW) signals~ analyzing all combinations of:
FC = 1, 4, 10, 20, 40, 60
SC = 100, 150, 200, 250, 300
FRAMA = 10, 20, 40, 80, 126, 252
Part of the FRAMA calculation involves finding the slope of prices for the first half, second half and the entire length of the FRAMA period. For this reason the FRAMA periods we tested were selected due to being even numbers and the fact that they correspond with the approximate number of trading days in standard calendar periods: 10 days = 2 weeks, 20 days = 1 month, 40 days = 2 months, 80 days = ⅓ year, 126 days = ½ year and there are 252 trading days in an average year. A total of 920 different averages were tested and each one was run through 300 years of data across 16 different global indexes (details here).
Download A FREE Spreadsheet With Raw Data For
All 920 FRAMA Long and Short Test Results
.
FRAMA – Test Results:
.
- Daily vs Weekly Data – EOD vs EOW Signals
- Annualized Return
- Annualized Return During Exposure
- Time In The Market
- Trade Duration
- Probability Of Profit
.
Daily vs Weekly Data – EOD vs EOW Signals
.
In our original MA test; Moving Averages – Simple vs. Exponential we revealed that once an EMA length was above 45 days, by using EOW signals instead of EOD signals you didn’t sacrifice returns but did benefit from a 50% jump in the probability of profit and double the average trade duration. To see if this was also the case with the FRAMA we compared the best returns produced by each signal type:
.
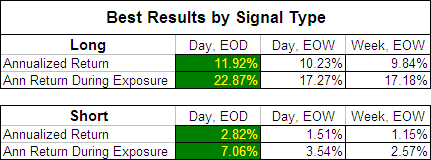
As you can see, for the FRAMA, Daily data with EOD signals produced by far the most profitable results and we will therefore focus on this data initially. It is presented below on charts split by FRAMA period with the test results on the “y” axis, the Fast MA (FC) on the “x” axis and a separate series displayed for each Slow MA (SC).
.
FRAMA Annualized Return – Day EOD Long
.

.
The first impressive thing about the results above is that every single Daily EOD Long average tested outperformed the buy and hold annualized return of 6.32%^ during the test period (before allowing for transaction costs and slippage). This is a strong vote of confidence for the FRAMA as an indicator.
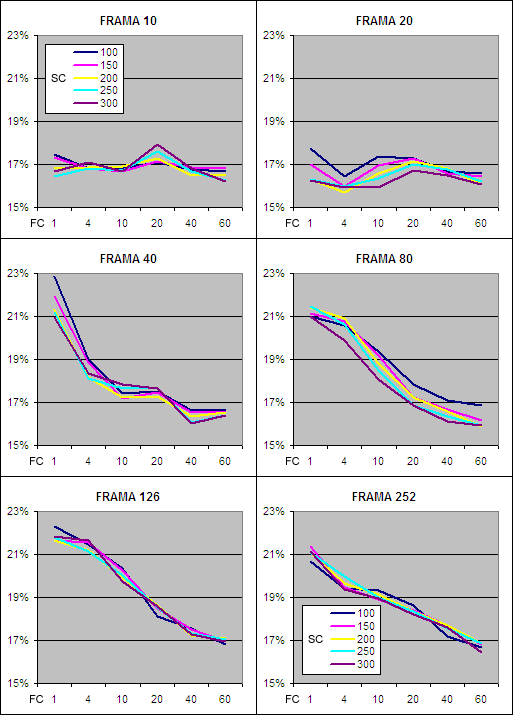
You will also notice that the data series on each chart are all bunched together revealing that similar results are achieved despite the “SC” period ranging from 100 to 300 days. Changing the other parameters however makes a big difference and returns increase significantly once the FRAMA period is above 80 days. This indicates that the Fractal Dimension is not as useful if measured over short periods.
When the FRAMA period is short, returns increase as the “FC” period is extended. This is due to the Fractal Dimension being very volatile if measured over short periods and a longer “FC” dampening that volatility. Once the FRAMA period is 40 days or more the Fractal Dimension becomes less volatile and as a result, increasing the “FC” then causes returns to decline.
Overall the best annualized returns on the Long side of the market came from a FRAMA period of 126 days which is equivalent to about six months in the market, while a “FC” of just 1 to 4 days proved to be most effective. Assessing the results from the Short side of the market comes to the same conclusion although the returns were far lower: FRAMA Annualized Return – Short.
.
FRAMA Annualized Return During Exposure – Day EOD Long
.
 .
.
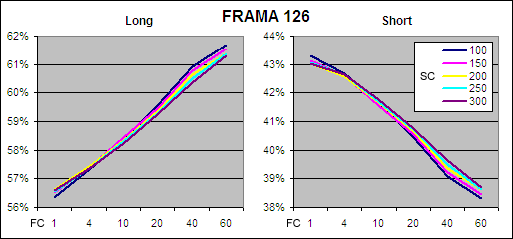
The above charts show how productive each different Daily FRAMA EOD Long was while exposed to the market. Clearly the shorter FRAMA periods are far less productive and anything below 40 days is not worth bothering with. The 126 day FRAMA again produced the best returns with the optimal “FC” being 1 – 4 days. Returns for going short followed a similar pattern but as you would expect were far lower; FRAMA Annualized Return During Exposure – Short.
Moving forward we will focus in on the characteristics of the 126 Day FRAMA because it consistently produced superior returns.
.
FRAMA, EOD – Time in Market
.
 .
.
Because the 16 markets used advanced at an average annualized rate of 6.32%^ during the test period it doesn’t come as a surprise that the majority of the market exposure was to the long side. By extending the “FC” it further increased the time exposed to the long side and reduced exposure on the short side. If the test period had consisted of a prolonged bear market the exposure results would probably be reversed.
.
FRAMA, EOD – Trade Duration
.
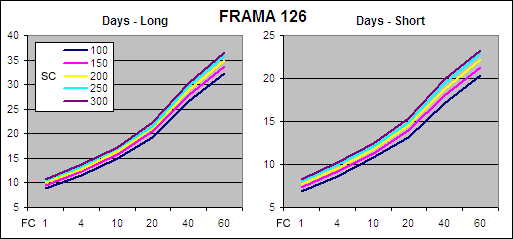
.
By increasing the “FC” period it also extends the average trade duration. Changing the “SC” makes little difference but as the “SC” is raised from 100 to 300 days the average trade duration does increase ever so slightly.
.
FRAMA, EOD – Probability of Profit
.
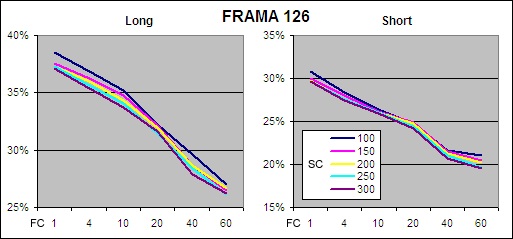
.
As you would expect, the probability of profit is higher on the long side which again is mostly a function of the global markets rising during the test period. However the key information revealed by the charts above is that the probability of profit decreases significantly as the “FC” is extended. This is another indication that the optimal FRAMA requires a short “FC” period.
.
The Best Daily EOD FRAMA Parameters
.
Our tests clearly show that a FRAMA period of 126 days will produce near optimal results. While for the “SC” we have shown that any setting between 100 and 300 days will produce a similar outcome. The “FC” period on the other hand must be short; 4 days or less. John Ehlers’ original FRAMA had a “FC” of 1 and a “SC” of 198; this will produce fantastic results without the need for any modification.
Because we prefer to trade as infrequently as possible we have selected a “FC” of 4 and a “SC” of 300 as the best parameters because these settings results in a longer average trade duration while still producing great returns on both the Long and Short side of the market:
.
FRAMA, EOD – Long
.
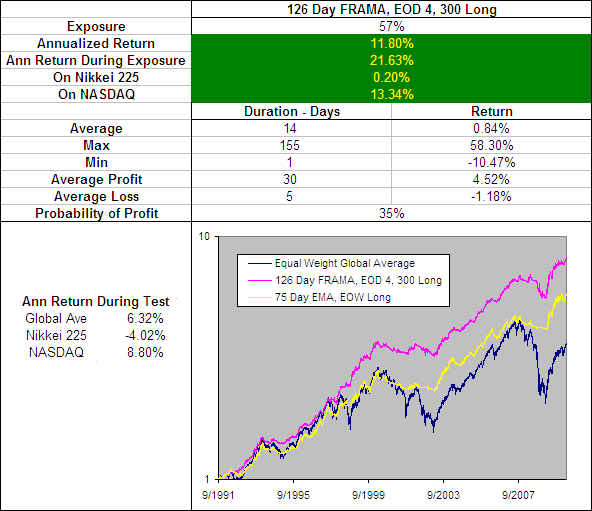
.
Above you can see how the 126 Day FRAMA with a “FC” of 4 and a “SC” of 300 has performed since 1991 compared to an equally weighted global average of the tested markets. I have included the performance of the 75 Day EMA, EOW becuase it was the best performing exponential moving average from our original tests.
This clearly illustrates that the Fractal Adaptive Moving Average is superior to a standard Exponential Moving Average. The FRAMA is far more active however producing over 5 times as many trades and did suffer greater declines during the 2008 bear market.
.
FRAMA, EOD – Short
.

.
On the Short side of the market the FRAMA further proves its effectiveness. Without needing to change any parameters the 126 Day FRAMA, EOD 4, 300 remains a top performer. When we ran our original tests on the EMA we found a faster average worked best for going short and that the 25 Day EMA was particularly effective. But as you can see on the chart above the FRAMA outperforms again.
What is particularly note worthy is that the annualized return during the 27% of the time that this FRAMA was short the market was 6.64% which is greater than the global average annualized return of 6.32%.
.
 See the results for the 126 Day FRAMA, EOD 4, 300
See the results for the 126 Day FRAMA, EOD 4, 300
Long and Short on each of the 16 markets tested.
.
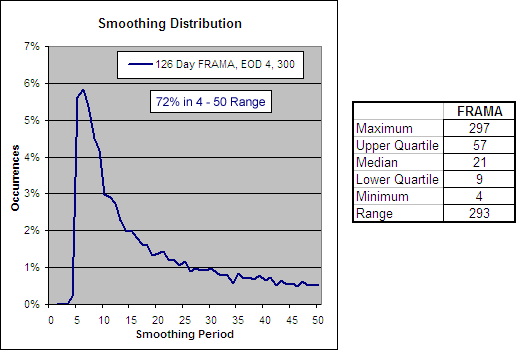
126 Day FRAMA, EOD 4, 300 – Smoothing Period Distribution
.
With a standard EMA the smoothing period is constant; if you have a 75 day EMA then the smoothing period is 75 days no matter what. The FRAMA on the other hand is adaptive so the smoothing period is constantly changing. But how is the smoothing distributed? Does it follow a bell curve between the “FC” and “SC”, is it random or is it localized around a few values. To reveal the answer we charted the percentage that each smoothing period occurred across the 300 years of test data:
.
 .
.
The chart above came as quite a surprise. It reveals that despite a “FC” to “SC” range of 4 to 300 days, 72% of the smoothing was within a 4 to 50 day range and the majority of it was only 5 to 8 days. This explains why changing the “SC” has little impact and why changing the “FC” makes all the difference. It also explains why the FRAMA does not perform well when using EOW signals, as an EMA must be over 45 days in duration before EOW signals can be used without sacrificing returns.
.
A Slower FRAMA
.
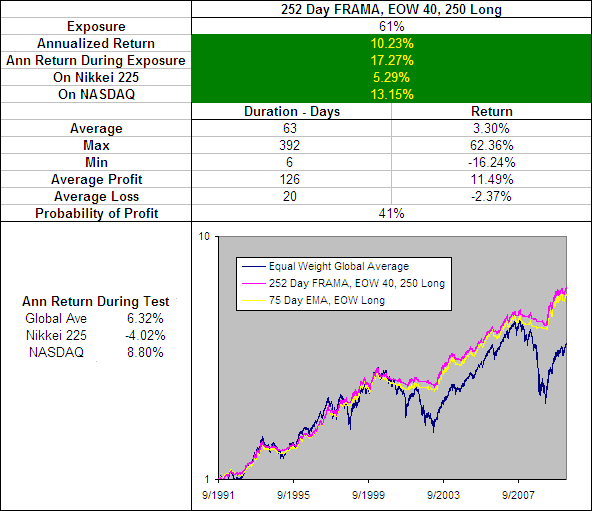
We have identified that the FRAMA is a very effective indicator but the best parameters (126 Day FRAMA, EOD 4, 300 Long) result in a very quick average that in your tests had an typical trade duration of just 14 days. We also know that the 75 Day EMA, EOW Long is an effective yet slower moving average and in our tests had a typical trade duration of 74 days.
A good slow moving average can be a useful component in any trading system because it can be used to confirm the signals from other more active indicators. So we looked through the FRAMA test results again in search a less active average that is a better alternative to the 75 Day EMA and this is what we found:
.
 .
.
The 252 Day FRAMA, EOW 40, 250 Long produces some impressive results and does out perform the 75 Day EMA, EOW Long by a fraction. However this fractional improvement is in almost every measure including the performance on the short side. The only draw back is a slight decrease in the average trade duration from 74 days to 63 when long. As a result the 252 Day FRAMA, EOW 40, 250 has knocked the 75 Day EMA, EOW out of the Technical Indicator Fight for Supremacy.
.
See the results for the 252 Day FRAMA, EOW 40, 250
Long and Short on each of the 16 markets tested.
.
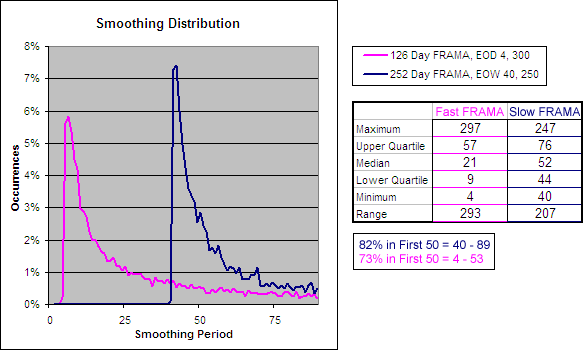
252 Day FRAMA, EOW 40, 250 – Smoothing Period Distribution
.
 .
.
.
FRAMA Testing – Conclusion
.
The FRAMA is astoundingly effective as both a fast and a slow moving average and will outperform any SMA or EMA. We selected a modified FRAMA with a “FC” of 4, a “SC” of 300 and a “FRAMA” period of 126 as being the most effective fast FRAMA although the settings for a standard FRAMA will also produce excellent results. For a slower or longer term average the best results are likely to come from a “FC” of 40, a “SC” of 250 and a “FRAMA” period of 252.
Robert Colby in his book ‘The Encyclopedia of Technical Market Indicators’ concluded, “Although the adaptive moving average is an interesting newer idea with considerable intellectual appeal, our preliminary tests fail to show any real practical advantage to this more complex trend smoothing method.” Well Mr Colby, our research into the FRAMA is in direct contrast to your findings.
It will be interesting to see if any of the other Adaptive Moving Averages can produce better returns. We will post the results HERE as they become available.
Well done John Ehlers you have created another exceptional indicator!
.
More in this series:
We have conducted and continue to conduct extensive tests on a variety of technical indicators. See how they perform and which reveal themselves as the best in the Technical Indicator Fight for Supremacy.
.
- ~ An entry signal to go long (or exit signal to cover a short) for each average tested was generated with a close above that average and an exit signal (or entry signal to go short) was generated on each close below that moving average. No interest was earned while in cash and no allowance has been made for transaction costs or slippage. Trades were tested using End Of Day (EOD) and End Of Week (EOW) signals for Daily data and EOW signals for Weekly data. Eg. Daily data with an EOW signal would require the Week to finish above a Daily Moving Average to open a long or close a short while Daily data with EOD signals would require the Daily price to close above a Daily Moving Average to open a long or close a short and vice versa.
- ^ This was the average annualized return of the 16 markets during the testing period. The data used for these tests is included in the results spreadsheet and more details about our methodology can be found here.