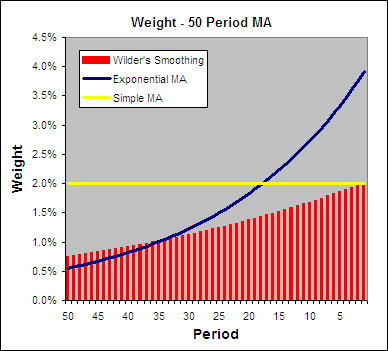
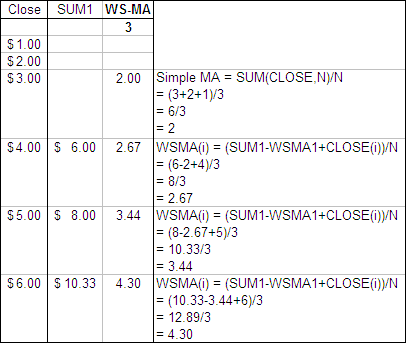
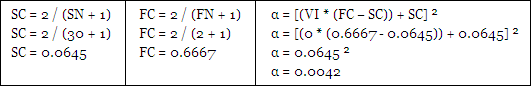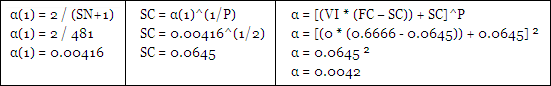The Log-Normal Moving Average (LAMA) is the name I have given to an Adaptive Moving Average that uses the adaptive process developed by John F Ehlers for use in his FRAMA. Stock prices are said to be Log-Normal so Ehlers used EXP to relate his Volatility Index (The Fractal Dimension) to Alpha. The LAMA is designed so that any VI can easily be incorporated as long as it shifts between a range of 1 – 0 where high readings indicate high volatility.
How to Calculate an Log-Normal Moving Average
Seed it with the Close price then after that the LAMA is calculated according to the following formula:
LAMA = LAMA(1) + New α * (Close – LAMA(1))
Where:
New α = 2 / (New N + 1)
New N = ((SC – FC) * ((N – 1) / (SC – 1))) + FC
SC = Your choice of a Slow moving average > FC
FC = Your choice of a Fast moving average < SC
N = (2 – α) / α
α = EXP(W * (1 – VI))
W = LN(2 / (SC + 1))
***If the above formula does not make a lot of sense to you and you would like a more in depth explanation then please read this article on the Fractal Adaptive Moving average.
Log-Normal Adaptive Moving Average Excel File
I have put together an Excel Spreadsheet containing the Log-Normal Adaptive Moving Average and made it available for FREE download. It contains a ‘basic’ version that shows all the working for the formula and a ‘fancy’ one that will automatically adjust to the length as well as the Volatility Index you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Log-Normal Adaptive Moving Average (LAMA)
How EXP affects Alpha and the Smoothing Period:
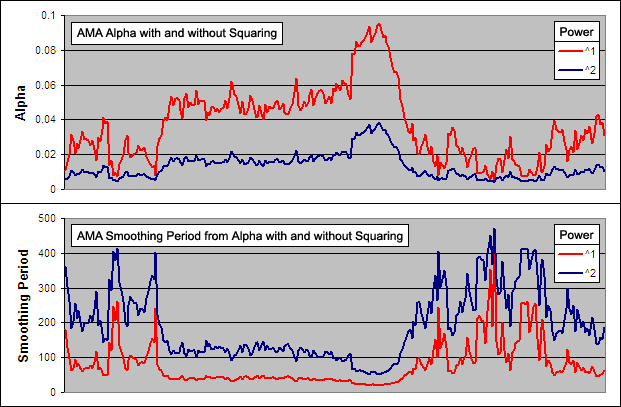
Ehlers used EXP to relate the Volatility Index (VI) to Alpha (α) so lets have a look at what affect this has:
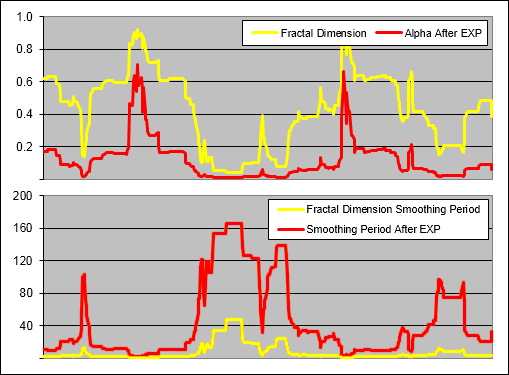 .
.
In the top chart you can see Alpha taken directly from the the Fractal Dimension and also taken after it has been modified by applying EXP. In the bottom chart you can see the smoothing period that results from each version of Alpha. Clearly by applying EXP, Alpha is reduced creating an significantly faster Smoothing Period.
The use of EXP results in not just a slower LAMA overall but one that exponentially slows as alpha decreases. This affect is similar to that of raising Alpha to a power as seen in the Adaptive Moving Average (AMA). In fact, it turns out that the LAMA is identical to the AMA if you were to raise it to the power of about 988,869,997.798!!!!!! That is not a typo. The LAMA and therefore the FRAMA is identical to the AMA raised the power of almost 100 million….
In discovering this there is little point in running the tests on this indicator because previous tests on the AMA already reveal it will not be able to out perform. Oh well, that saves some work! That is why we take the time to look closer at these things and try not to make too many uneducated assumptions.
More in this series:
We have conducted and continue to conduct extensive tests on a variety of technical indicators. See how they perform and which reveal themselves as the best in the Technical Indicator Fight for Supremacy.