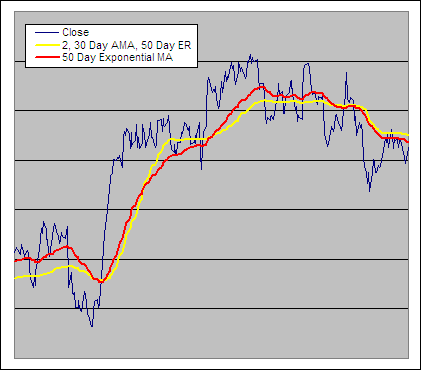
The Adaptive Moving Average (AMA) aka Kaufman Adaptive Moving Average (KAMA) was created by Perry Kaufman and first presented in his book Smarter Trading (1995). This moving average offered a significant advantage over previous attempts at ‘intelligent’ averages because it allowed the user greater control.
The Variable Moving Average – VMA (1992) for instance offered no upper or lower limit to its smoothing period. The AMA on the other hand allowed the user to define the range across which they desired the smoothing to be spread.
It follows the same theory as the VMA in that depending on the market environment there will be different amounts of noise and therefore a different moving average speed will be required to achieve the most profitable results. In a strongly trending market for instance, the noise levels are low and a faster moving average should produce the best results. Conversely in a crab or sideways market the noise levels are very high and a slower average is likely to be better suited.
.
How to Calculate an Adaptive Moving Average
.
It starts with the Close price.
AMA(1) = Close
After that AMA is calculated according to the following formula:
AMA = AMA(1) + α * (Close – AMA(1))
You will notice that this is the same as the formula for an Exponential Moving Average (EMA):
EMA = EMA(1) + α * (Close – EMA(1))
But Alpha in an EMA is α = 2 / (N + 1) so it remains constant while for an AMA the Alpha is adaptive:
α = [(VI * (FC – SC)) + SC] ²
Where:
VI = Users choice of a measure of volatility or trend strength, Kaufman suggested his Efficiency Ratio (ER).
SC = 2 / (SN + 1)
SN = Your choice of a Slow moving average > FN
FC = 2 / (FN + 1)
FN = Your choice of a Slow moving average < SN
Here is an example of a 3 period AMA with a 3 period Efficiency Ratio (ER) as the VI:
.
 .
.
How Squaring Alpha affects the AMA Smoothing Range
.
Kaufman suggest that his AMA have a FC of 2 and a SC of 30 which would lead one to assume that the adaptive smoothing would be in the 2 – 30 range but you would be wrong because the alpha is squared. For example, lets set the VI to zero so we can reveal the slowest possible average:
.
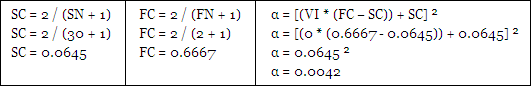 .
.
Now to reveal the EMA smoothing period ‘N’ from alpha:
N (EMA) = (2 – α) / α
N (EMA) = (2 – 0.0042) / 0.0042
N (EMA) = 480
So in reality an AMA with a SN of 30 where alpha is raised to the power of 2 can actually move as slowly as a 480 day EMA. Now to me that is not very user friendly; entering a parameter of 30 that results in a smoothing period of 480. So I use the following formula for SC and FC instead:
SC = α(1)^(1/P)
Where:
α(1) = 2 / (SN+1)
P = Power that alpha is raised to (usually 2)
SN = Your choice of a Slow moving average > FN
Now SN will be the actual resulting slowest moving average even if you change the power that alpha is raised to. I also use the same process for FN and FC. Lets look again at Alpha with the VI set to zero, the FN at 2 and the SN at 480:
.
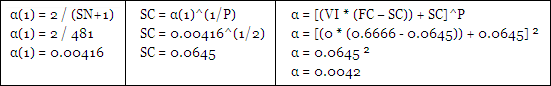 .
.
Now when we reveal the EMA smoothing period ‘N’ from alpha it should equal our user defined 480:
N (EMA) = (2 – α) / α
N (EMA) = (2 – 0.0042) / 0.0042
N (EMA) = 480
.
A closer look at the affect of Squaring Alpha
.
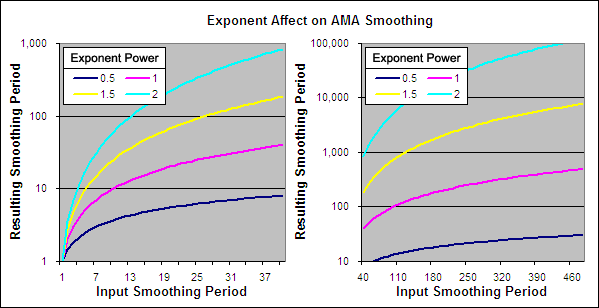
Understanding the affect of squaring alpha is very important as the chart below illustrates:
.
.
As you can see above, an input smoothing period of 300 with alpha squared results in an actual smoothing period of over 45,300 which is totally useless. However this is a setting that one could easily use without a proper understanding of how the AMA works. In our testing we will be trying the AMA with alpha raised to powers other that 2 so some other examples have also been plotted on the chart above.
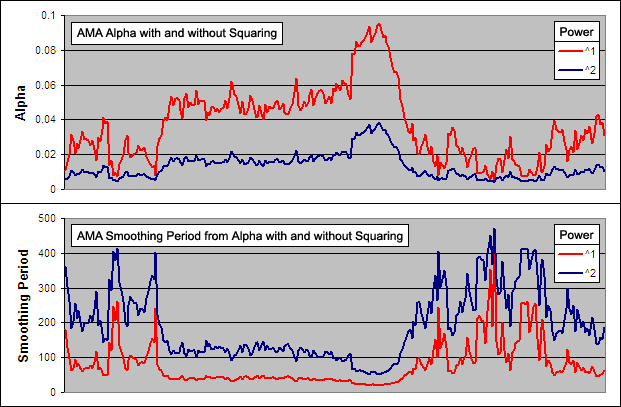
Below we look at the affect on alpha and the smoothing resulting from an AMA with the Efficiency Ratio taken directly into alpha (^1) or being squared (^2):
.
.
We used our modified AMA formula for the above charts so that the actual FN and SN were identically matched despite modifications to alpha. As you can see, squaring alpha results in not just a slower AMA overall but one that is much faster to slow down when the alpha decreases. Kaufman obviously wanted the AMA to very rapidly slow when the data lacked a trend. This affect is similar to that of increasing the constant ‘N’ in the Variable Moving Average.
.
Is the AMA a Good Indicator?
.
As part of the ‘Technical Indicator Fight for Supremacy‘ we will be putting the AMA against several different types of moving averages and will test several different Volatility Indexes as components including:
- Kaufman’s Efficiency Ratio (ER) – Completed – Results
- Fractal Dimension (D) = ABS(D – 2) – Completed – Results
- Standard Deviation Ratio (SDR) – Completed – Results
- Relative Volatility Index (RVI) = RVI/100 – Completed – Results
- Vertical Horizontal Filter (VHF) – Completed – Results
- Chaikin’s Volatility (CV) * We currently lack High and Low Prices for some test markets.
We will also be testing the assumption that squaring alpha was a good idea and will try raising it to several different powers.
Can you think of any other worthwhile tests? Please let us know in the comments section at the bottom.
.
Adaptive Moving Average Excel File
.
I have put together an Excel Spreadsheet containing the Adaptive Moving Average and made it available for FREE download. It contains a ‘basic’ version that shows all the working and a ‘fancy’ one that will automatically adjust to the length as well as the Volatility Index you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Adaptive Moving Average (AMA)
.
Adaptive Moving Average Example, VI = 50 Day Efficiency Ratio
.