FRAMA stands for Fractal Adaptive Moving Average and we have classed it as a Log-Normal Adaptive Moving Average (LAMA). Created by John F Ehlers (See his original paper or the article from the 2005 edition from Technical Analysis of Stocks and Commodities – Fractal Adaptive Moving Averages), it utilizes Fractal Geometry in an attempt to dynamically adjust its smoothing period to suit the changing price action over time. The FRAMA theory is extremely clever, but clever theories don’t guarantee good results so we are putting the concept into the ring for the ‘Technical Indicator – Fight for Supremacy‘.
But before we go any further it is important that we understand what we are testing. So I will explain how the FRAMA works although I must admit it is a bit above the the maths education that I didn’t pay attention to in school. Also we have put together a free excel spreadsheet containing the Fractional Adaptive Moving Average so you can test it for yourself.
(If you would rather skip the maths then jump to the completed test results here – Is the FRAMA Effective?)
.
FRAMA Topics
.
- How The FRAMA Works
- How to Calculate a Fractal Adaptive Moving Average
- What is Log-Normal and why does it describe stock prices?
- How to Calculate a Fractal Adaptive Moving Average – Continued
- Finding The Fractal Dimension, Examples
- How does the Fractal Dimension “D” affect the smoothing period “N”?
- Modified FRAMA
- FRAMA Excel File
- FRAMA and a Simple Moving Average
Test Results – Is the FRAMA Effective?
.
How The FRAMA Works
.
First of all the FRAMA takes advantage of the fact that financial markets are fractal. A fractal shape is said to be rough or fragmented and can be split into parts, each of which is at least similar to a reduced size copy of the original. Example: Can you see anything strange about the chart below?
.
.
Without being told would you have known that the left half of the chart above was 5 years of monthly bars and the right half was 15 days on 30 minute bars? Probably not, because price movements look similar no matter what time frame we are viewing them in. This characteristic is called self-similarity and defines a fractal shape.
By finding the Fractal Dimension or “D” we get an indication as to how completely a Fractal appears to fill space as one zooms down to finer and finer scales. Think of it this way: A stock chart is too big to be one dimensional but too thin to be two dimensional so its Fractal Dimension is a reading between one and two.
(For a more in depth look into Fractals and “D” please read this post – The Fractal Dimension)
The FRAMA identifies the Fractal Dimension of prices over a specific period and then uses the result to dynamically adapt the smoothing period of an exponential moving average.
.
Finding The Fractal Dimension of a Shape
.
To find the Fractal Dimension “D” of a shape we cover it with a number “F” of small objects that are various sizes “S”:
D = Log(F2 / F1) / Log(S1 / S2)
What is Log?
For those of you like me who didn’t pay attention in maths class ‘Log’ is short for Logarithm and is the power that a number needs to be raised to in order to produce a given result. Unless otherwise stated the base number is 10, therefore:
Log(1000) = 3
Because
10^3 = 10 * 10 * 10
10^3 = 1000
After that quick maths lesson lets calculate the Fractal Dimension for a line segment that is 10 meters long. First select two small dimensions such as S1 = 1 meter and S2 = 0.1 meters. By placing boxes of these sizes on the line segment we can fit 10 of the one meter size and 100 of the 0.1 meter size. So F1 = 10 and F2 = 100. Therefore:
D = Log(F2 / F1) / Log(S1 / S2)
D = Log(100 / 10) / Log(1 / 0.1)
D = Log(10) / Log(10)
D = 1 / 1
D = 1
Because D = 1 we have revealed that the Fractal exists fully in one Dimension which makes sense because the measured shape was just a flat line.
For a second example instead of a flat line lets use a square that is 10 x 10 meters. Keeping S1 and S2 the same we now get F1 = 100 and F2 = 10,000 therefore:
D = Log(F2 / F1) / Log(S1 / S2)
D = Log(10,000 / 100) / Log(1 / 0.1)
D = Log(100) / Log(10)
D = 2 / 1
D = 2
Because D = 2 we have revealed that the Fractal has completely filled two dimensions which makes sense as the measured shape was a square and a square requires two dimensions to exist.
Unfortunately stock prices lack this regularity but are still self similar. So, in order to discover the “D” of stock prices we must average the measured Fractal Dimension over different scales.
Covering a price curve with a series of small boxes is far too cumbersome but because price samples are uniformly spaced (each bar is 1 day, 1 week, 10 min etc) Ehlers decided that the average slope of the curve could be used as an estimation of the box count. This is far less complicated than it sounds as the slope is found by simply taking the highest price over a period minus the lowest price during that period and dividing the result by the number of periods. We will call this measure “HL”, therefore:
HL = (Max(High,N) – Min(Low,N)) / N
N = Periods
We will need to find the “HL” measure (slope) over the first half, second half and full length of “N” to help us find “D”, clear as mud?
.
How to Calculate a Fractal Adaptive Moving Average
.
It starts with the Close price.
FRAMA(N-1) = Close
After that FRAMA is calculated according to the following formula:
FRAMA = FRAMA(1) + α * (Close – FRAMA(1))
You will notice that this is the same as the formula for an Exponential Moving Average (EMA):
EMA = EMA(1) + α * (Close – EMA(1))
But Alpha in an EMA is α = 2 / (N + 1) so it remains constant while for the FRAMA α = EXP(W*(D – 1)) making it adapt as the Fractal Dimension changes.
What is EXP?
EXP is known as the Exponential Function, it is like Log but instead of an assumed base of 10 it has a base of “e”. So x = Log(10^x) and x = EXP(e^x) where “e” is approximately 2.718281828. Confused yet? “e” is a unique number because the slope of its curve is 1 when x = 0 and it solves the compound interest problem.
Didn’t know there was a problem with compound interest? Neither did I.
You see if you invest $1 at an interest rate of 100% calculated annually, at the end of the first year you will have $2; simple. But if you compound the interest during the year it gets a bit more complicated. When interest is compounded every 6 months you can find the result for the year by multiplying $1 by 1.5 twice, so $1.00 × 1.5^2 = $2.25. If the interest is compounded quarterly then the result is $1.00 × 1.25^4 = $2.44, and monthly it is $1.00 × 1.0833…^12 = $2.613035….
Notice how each time you increase the frequency of compounding you get a larger result? This is the ‘compound interest problem’. However if you invest $1 with a return of 100% each year and the interest is compound constantly then the result is ‘e’.
So why did Ehlers use EXP?
If a number “Y” has a random variable with a Normal Distribution then EXP(Y) has a Log-Normal Distribution. Stock prices are said to be Log-Normal so EXP is used to relate the Fractal Dimension to Alpha. Keep reading this will make more sense soon…
What is Log-Normal and why does it describe stock prices?
(In theory) the percentage change to achieve possible future stock prices at the end of a period is Normally Distributed. That is; the change will result in a positive or negative return and 95% of the outcomes should fall within two standard deviations of the mean. (In reality price changes aren’t normally distributed – Michael Stokes explains Fat Tails)
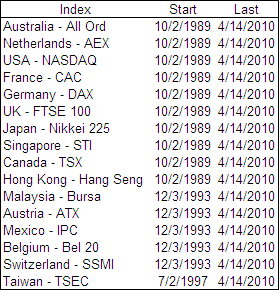
The possible prices that will result from those changes can range from zero and infinity. This is because a stock can’t drop more than 100% as that would result in a negative price but a it can more than double. Therefore prices are said to be Log-Normal. This concept really confused me at first but a picture is worth a 1000 words so:
.
.
To show that stock prices are roughly Log-Normal I calculated the price change over the prior year for the last 10,000 market days on the Dow. In theory these results are Normally Distributed so by finding their EXP and plotting the frequency each result occurs, the above chart reveals the most probable closing prices for the Dow in one years time.
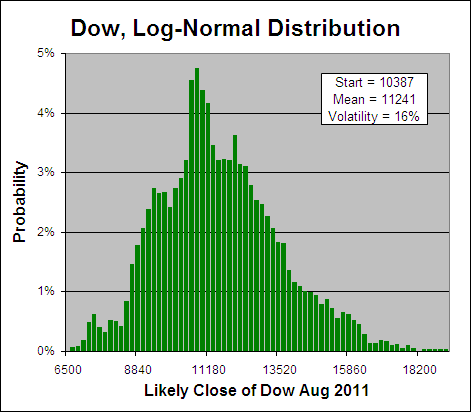
Now if a number “Y” is Log-Normal, then Log(Y) will be Normally Distributed. So if stock prices are indeed Log-Normal then by taking the Log of the price changes on the above chart we should get something that looks like a bell curve:
.
.
Above you can see a bell curve (all be it an ugly one) that displays the probability of any percent chance on the Dow over the next year between -20% and 25%. So hopefully that explains what Log-Normal is and why it is a characteristic of stock prices… Here ends the maths lesson.
.
How to Calculate a Fractal Adaptive Moving Average – Continued
.
FRAMA = FRAMA(1) + α * (Close – FRAMA(1))
Where:
α = EXP(W * (D – 1))
D = (Log(HL1 + HL2) – Log(HL)) / Log(2)
Note: Log(2) = Log(N / (½N))
HL1 = (Max(High,½N..N) – Min(Low,½N..N)) / ½N
HL2 = (Max(High,½N) – Min(Low,½N)) / ½N
HL = (Max(High,N) – Min(Low,N)) / N
N = FRAMA Period, must be an even number.
W = -4.6 (Set by Ehlers but can be changed. See: Modified FRAMA)
If Alpha < 0.01 then Alpha = 0.01
If Alpha > 1 then Alpha = 1
.
Finding The Fractal Dimension, Examples
.
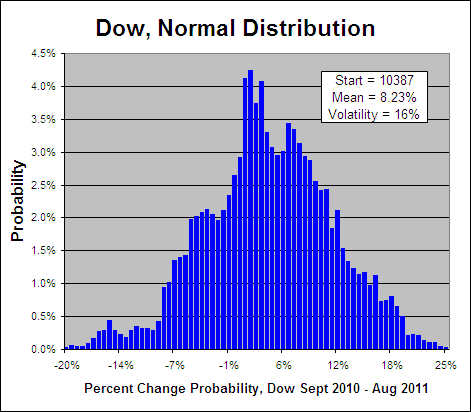
Lets have a look at some theoretical stock prices and the resulting Fractal Dimension:
.
.
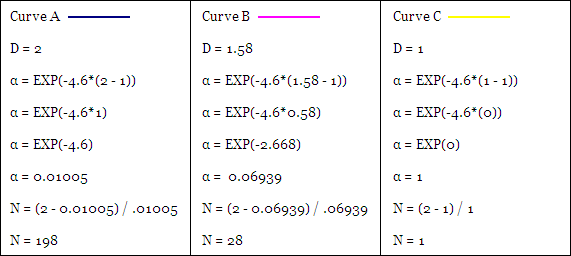
Above are three price curves, now lets calculate the “D” for each where “N” = 100.
D = (Log(HL1 + HL2) – Log(HL)) / Log(2)
So:
.
For ‘Curve A’ the full range is repeated in both halves of the chart so it exists fully in two Dimensions and D = 2. For ‘Curve B’ only half of the range is repeated in each half of the chart so it exists in between one and two Dimensions or specifically D = 1.58. The range for ‘Curve C’ is not repeated at all between the two halves of the chart so it exists in only one Dimension and D = 1.
.
How does the Fractal Dimension “D” affect the Smoothing Period “N”?
.
The FRAMA adapts between being a Fast or Slow EMA based in the Fractal Dimension of stock prices. Ehlers designed the slowest possible EMA to be approximately 200 periods in duration and the fastest to have a period of one or in other words be equal to the price itself. So for the three curves from our previous example, lets see how “D” changes “α” and how that affects “N” or the smoothing period of the resulting EMA:
α = EXP(W*(D – 1))
N (EMA) = (2 – α) / α
(Ehlers set “W” as -4.6, but it can be changed. See: Modified FRAMA)
.
.
When D = 2 as with ‘Curve A’ the result is an Slow EMA of 198 periods while when D = 1 as with ‘Curve C’ the result is a Fast EMA of one period (the close price itself).
.
“This adaptive structure rapidly follows major changes in price and slowly changes when the prices are in a congestion zone.” – John Ehlers
.
Modified FRAMA
.
Ehlers rigidly set the FRAMA to shift between a Fast EMA of 1 period (lets call it FC) and a Slow EMA of 198 days (lets call it SC). But because we are going to be entering the FRAMA in the ‘Technical Indicator – Fight for Supremacy‘ I wanted to be able to specifically define the “FC” and “SC” of my choice.
Special thanks to Prospectus – “Real Rocket Scientist, Wanna-be Trader” for his help on this section, be sure to subscribe to his blog and follow him on twitter.
So instead of setting “W” as -4.6 as Ehlers did, lets make W = LN(2 / (SC + 1)). This results in a FRAMA that shifts between a “FC” of 1 and a “SC” of your choice. For example where SC = 200, W = -4.61015. Ehlers obviously rounded this off hence his setting of -4.6.
What is LN and why do we use it to find “W”?
LN is an abbreviation for ‘Natural Logarithm’ and is the inverse of EXP; so if EXP(1) = x then LN(x) = 1. Because EXP is used to relate the Fractal Dimension to Alpha, LN is used to find “W”.
Now in order to set the Fast MA or “FC” of your choice simply take the resulting EMA period “N” and adjust it to fit the new range. For example if SC = 100 and the resulting N = 50 but instead of the standard SC = 1 we want to change it to SC = 20, the following formula will reveal the “New N”:
New N = ((SC – FC) * ((Origional N – 1) / (SC – 1))) + FC
New N = ((100-20) * ((50 – 1) / (100 – 1))) + 20
New N = (80 * (49 / 99)) + 20
New N = 60
This is then easily converted back into Alpha: New α = 2 / (New N + 1)
Modified FRAMA additional rules:
SC = Your choice of a Slow moving average > FC
FC = Your choice of a Fast moving average < SC
If Alpha < 2 / (SC + 1) then Alpha = 2 / (SC + 1)
If Alpha > 1 then Alpha = 1
FRAMA(N-1) = SUM(CLOSE, H)/H
H = EVEN( ((SC – FC) / 2) ) + FC
If N-1 < EVEN( ((SC – FC) / 2) ) + FC then H = N-1
.
FRAMA Excel File
.
We have put together an Excel Spreadsheet containing the FRAMA and made it available for FREE download. It contains a ‘basic’ version of John Ehlers FRAMA and our Modified version along with a ‘fancy’ one that will automatically adjust to the settings that you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Fractal Adaptive Moving Average (FRAMA). Please let me know if you find it useful.
.
FRAMA and a Simple Moving Average
.
.
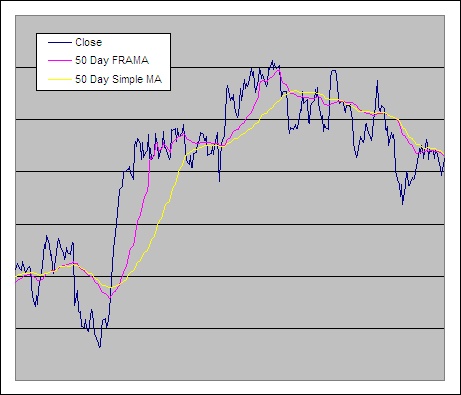
Fractal Adaptive Moving Average Test Results
.
We tested the FRAMA through 300 years of data across 16 global markets, see the results now – Is the FRAMA Effective?
.
.
.
There are a vast number of technical indicators out there but which ones are best? Are any of them suitable for use in a mechanical trading model? Do any of them actually provide value over a buy and hold approach? In my experience most of the publicly available technical indicators are of little, if any value. All of our best performing models are build on completely new ideas that deviate from conventional approaches to technical analysis almost entirely.