Technical Indicator – Page 2

Standard Deviation Ratio (SDR)

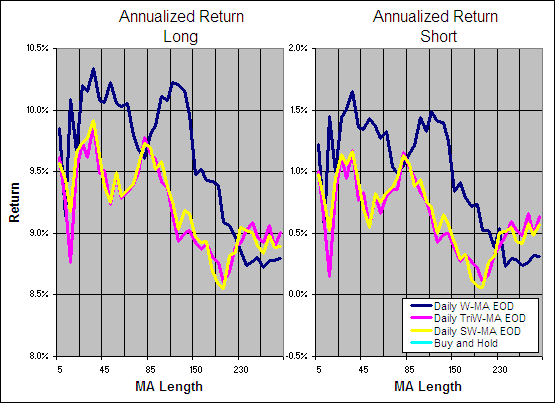
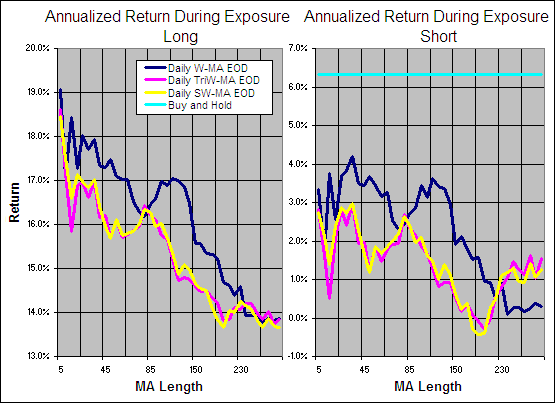
The Standard Deviation Ratio (SDR) was first presented as a technical indicator in the March 1992 edition of Technical Analysis of Stocks & Commodities magazine ‘Adapting Moving Averages To Market Volatility‘. The author Tushar S. Chande, Ph.D. used it as the Volatility Index in the original version of his Volatility Index Dynamic Average (VIDYA) or Variable Moving Average (VMA).

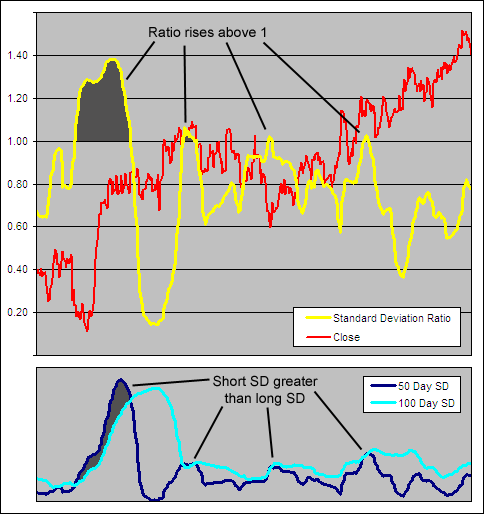
Calculating it is as simple as taking the ratio of a Standard Deviation (SD) over one period to that of a longer period where both have the same starting point. One quirk of the SDR is that because the short term SD can become greater than the longer term SD, the ratio has no upper limit but does tend to remain below 1 most of the time (see the example chart below). The higher the ratio, the more spread the recent data is from the mean in relation to the past which should indicate a stronger trend.

It is very helpful to know the strength or lack of a trend as different approaches will be more profitable depending on the market type. But is the Standard Deviation Ratio an effective way to reveal the strength of a trend? To find out we are entering it in the Technical Indicator Fight for Supremacy. We will be testing the SDR as a component in the VIDYA, an Adaptive Moving Average and an Indicator Weighted Moving Average.

50 / 100 Standard Deviation Ratio Example

Standard Deviation Ratio

Standard Deviation Ratio Excel File

I have put together an Excel Spreadsheet containing the Standard Deviation Ratio and made it available for FREE download. While the SDR may be very easy to calculate this spreadsheet will automatically adjust to the parameters you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Standard Deviation Ratio (SDR)

Test Results

.
As part of the ‘Technical Indicator Fight for Supremacy‘ We have tested/will test the Efficiency Ratio as a component in several technical indicators:

Standard Deviation Ratio Variable Moving Average (SDR-VMA) – Completed – Results
Standard Deviation Ratio Adaptive Moving Average (SDR-AMA) – Completed – Results
Standard Deviation Ratio Log Normal Adaptive Moving Average (SDR-LAMA)
Standard Deviation Ratio Weighted Moving Average (SDR-WMA)

We will also test the SDR as a filter, only taking trades when it indicates a strong trend.

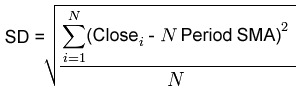
Standard Deviation

Standard Deviation (SD) reveals how much a data set varies from its mean; a high Standard Deviation indicates that the data is widely spread. With stock prices it can be used as a measure of the historical volatility to reveal the theoretical probability of a price change over a specified period. This information can be used in many ways such as a measure of risk or as a component in technical indicators.

Normal Distribution Bell Curve

Normal Distribution - Bell Curve .

A data set that is Normally Distributed with produce a probability curve called a bell curve, like the one above. One standard deviation from the mean accounts for 68% of the occurrences while two SDs covers 95% and three covers 99.7%. One of the challenges with the stock market is that the data is not Normally Distributed but instead exhibits Fat Tails. So the Standard Deviation is far from a perfect measure but is still a useful trading tool in some applications.

How To Calculate Standard Deviation

Standard deviation is the square root of variance and can easily be calculated in an Excel spread sheet with the =STDEVP() function or it can be done the hard way using the following formula:

Standard Deviation Formula

Where:

SMA = Simple Moving Average

N = Number of periods

Standard Deviation Example

If we take the percentage change of the Dow Jones Industrial Average for the 10 years from 2000 – 2010 we get the following values:

-6.17%, -7.1%, -16.76%, 25.32%, 3.15%, -0.61%, 16.29%, 6.43%, -33.84%, 18.82%

To find the SD we first find the mean (average):

(-6.17% + -7.1% + -16.76% + 25.32% + 3.15% + -0.61% + 16.29% + 6.43% + -33.84% + 18.82%) / N

= 5.53% / 10

= 0.55%

We then calculate the deviation of each data point from the mean (= Data Point – Mean), square the result and find the sum:

-6.72%^2 + -7.66%^2 + -17.32%^2 + 24.77%^2 + 2.6%^2 + -1.16%^2 + 15.73%^2 + 5.88%^2 + -34.39%^2 + 18.27%^2

= 28.24%

Finally divide the result by N to find the average and take the square root to reveal the SD

= √(28.24% / 10)

= 16.8%

This means that in theory (assuming a normal distribution), based on ten years of the Dow’s annual price changes, about 68% of years the Dow will move up or down within 16.8% (one standard deviation). While about 95% of years the Dow should finish up or down within 33.6% (two standard deviations).

What Does Standard Deviation Mean?
1. A measure of the dispersion of a set of data from its mean. The more spread apart the data, the higher the deviation. Standard deviation is calculated as the square root of variance.

2. In finance, standard deviation is applied to the annual rate of return of an investment to measure the investment’s volatility. Standard deviation is also known as historical volatility and is used by investors as a gauge for the amount of expected volatility.

Investopedia explains Standard Deviation
Standard deviation is a statistical measurement that sheds light on historical volatility. For example, a volatile stock will have a high standard deviation while the deviation of a stable blue chip stock will be lower.

Double Vs Triple Exponential Moving Average

In this round of testing we are looking at the Double Exponential (D-EMA) and Triple Exponential Moving Averages (T-EMA). We have already tested the D-EMA and found that it wasn’t as effective as the EMA but wanted to test it over longer periods and compare it to the T-EMA.

In conducting these tests we measured the performance of each indicator going Long and Short, using Daily and Weekly data, taking End Of Day (EOD) and End Of Week (EOW) signals with smoothing periods varying from from 5 – 400 days or 80 weeks.~ These tests were carried out over a total of 300 years of data across 16 different global indexes (details here).

Note – Due to the huge lead in period required for the T-EMA, 240 weeks of data was ‘left in’ on each market. As a result the average buy and hold annualized return for the test markets was 4.94%. In our previous tests we only ‘left in’ 104 weeks and the subsequent buy and hold annualized return for the test markets was 6.32%. For this reason the results for these tests are not directly comparable to our other tests results. This is also why the returns for the D-EMA displayed below are lower than those previously published.

Triple and Double Exponential MA Annualized Return

Above are the return statistics when going long using daily, end of day signals. As you can see the Triple EMA under performs the Double EMA by a significant margin. Due to the fact that we have already established that the D-EMA is not worthy of use in a trading system the same can be said for the T-EMA and therefore there is no point in displaying any more statistics for these indicators. See also – Simple Vs Exponential Moving Averages

~ An entry signal to go long (or exit signal to cover a short) for each average tested was generated with a close above that average and an exit signal (or entry signal to go short) was generated on each close below that moving average. No interest was earned while in cash and no allowance has been made for transaction costs or slippage. Trades were tested using End Of Day (EOD) and End Of Week (EOW) signals for Daily data and EOW signals only for Weekly data. Eg. Daily data with an EOW signal would require the Week to finish above a Daily Moving Average to open a long or close a short and vice versa.

Double (D-EMA) and Triple Exponential Moving Average (T-EMA)

The Double and Triple Exponential Moving Average were created by Patrick Mulloy and first published in the February 1994 issue of Technical Analysis of Stocks & Commodities magazine – Smoothing Data With Less Lag. Mulloy stated in his article:

“Moving averages have a detrimental lag time that increases as the moving average length increases. The solution is a modified version of exponential smoothing with less lag time.”

Like an EMA, the D-EMA and T-EMA apply more weight to the most recent data in an attempt to smooth out noise while still remaining highly reactive to changes in the data. This is not achieved by simply double and triple smoothing as one may assume. To do so results in weighting that resembles a backwards log-normal distribution, rather like a Triangular Moving Average but smooth and shifted forward. Below you can see how the weighting is allocated by a single, double and triple smoothed exponential moving average compared to a standard EMA and SMA:

Double and Tripple Smoothed EMA Weighting .

As you can see by double and triple smoothing an EMA the weighting no longer focuses on the latest data. The actual Double and Triple Exponential Moving Average applies the weighing very heavily to the most recent data as illustrated in the chart below:

Double and Tripple EMA Weight

How To Calculate a Double Exponential Moving Average and T-EMA

Double Exponential MA Formula:

D-EMA = 2*EMA – EMA(EMA)

Triple Exponential MA Formula:

T-EMA = (3*EMA – 3*EMA(EMA)) + EMA(EMA(EMA))

Where:

EMA = EMA(1) + α * (Close – EMA(1))

α = 2 / (N + 1)

N = The smoothing period.

Here is an example of a 3 period Double Exponential Moving Average and Triple EMA:

Double and Triple Exponential Moving Average Formula .

Triple Exponential Moving Average and D-EMA Excel File

We have built a spreadsheet to calculate the D-EMA and T-EMA and have made it available for free download. Find the file at the following link near the bottom of the page under Downloads – Technical Indicators: Double (D-EMA) and Triple Exponential Moving Average (T-EMA).

Double EMA, Triple EMA and a Simple Moving Average

Double and Tripple EMA Vs a Simple MA .

Double and Triple Exponential Moving Average Test Results

We ran them through tests through over 300 years of data across 16 different global markets. Here are the results:

Double Exponential Moving average Vs Simple and Exponential Moving average

Double Vs Triple Exponential Moving Average

More in this series:

We have conducted and continue to conduct extensive tests on a variety of technical indicators. See how they perform and which reveal themselves as the best in the Technical Indicator Fight for Supremacy.

Triangular Simple Moving Average (TriS-MA)

The Triangular Simple Moving Average (TriS-MA) is almost identical to the Triangular Weighted Moving Average but is very different in how it is calculated. Instead of weighting the data points directly it is a double smoothed simple moving average (a moving average of a moving average). Because most of the weight ends up being placed on the data in the middle of a series the weighting looks like a triangle, hence the name. Below you can see how the weighting is applied to a 50 period TriS-MA, EMA and SMA:

Triangular Simple MA vs SMA and EMA Weighting .

How To Calculate a Triangular Simple Moving Average

TriS-MA = SUM(MA1,L) / L

Where:

MA1 = SUM(CLOSE,L) / L

L = ceiling((n+1) / 2)

n = Number of Periods

Here is an example of a 3 period Triangular Weighted Moving Average:

How to Calculate a Triangular Simple Moving Average

Triangular Simple Moving Average Excel File

An Excel Spreadsheet containing a Triangular Weighted Moving Average is available for FREE download. It contains the ‘basic’ version you can see above and a ‘fancy’ one that will automatically adjust to the length you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Triangular Weighted Moving Average (TriW-MA). Please let us know if you find it useful.

Triangular Moving Average and a Simple Moving Average

50 Day Triangular Simple MA and Simple MA .

Test Results

We tested several different types of Moving Averages including the TriS-MA through 300 years of data across 16 global markets to reveal which is the best and if any of them are worth using in your trading – see the results.

Mixed Moving Averages – Test Results

In this round of testing we will be looking at a mix of different smoothing methods and averages: The Moving Linear Regression or Time Series Forecast (TSF) and The Linear Regression Indicator (LRI) which aren’t actually moving averages but can be used in the same way. Plus Wilder’s Smoothing AKA Smoothed MA (WS-MA) and the Triangular Simple MA (TriS-MA). The aim is to identify if any of these indicators are worth using as a trading tool.

We tested each indicator going Long and Short, using Daily and Weekly data, taking End Of Day (EOD) and End Of Week (EOW) signals with smoothing periods varying from from 5 – 300 days or 60 weeks.~ These tests were carried out over a total of 300 years of data across 16 different global indexes (details here).

Annualized Return Mixed Moving Averages

Above you can see the annualized return statistics for each indicator. The first thing that you will notice is that the LRI and TSF produce very similar results and neither of them are very good. So for providing buy signals in this fashion the Time Series Forecast and The Linear Regression Indicator are knocked out cold in the first round.

The returns generated by the TriS-MA are reasonable but they are not good enough to out perform the EMA’s results so the Triangular Simple Moving Average is also knocked out of contention. (Note – It didn’t dawn on us that the TriS-MA is almost identical to the Triangular Weighted Moving Average until after we had already tested it).

Wilder’s Smoothing produced some good returns when the smoothing period was less than 45 days but the performance dropped gradually to almost 7% as the length was extended. The EMA exhibited similar behavior but bottomed out around 8% so while Wilder’s Smoothing is effective in this application, the Exponential Moving Average is still King.
.

Best Average of the Group – Long

We performed a total of 948 tests in this round; half of them on the long side and half on the short. Rather than simply selecting the indicator with the greatest returns over the test period we identified the best for going long using the following criteria:

Annualized Return > 9%
Average Trade Duration > 29 Days
Annualized Return During Exposure > 15%
Annualized Return on Nikkei 225 > 3%

14/357 Averages made the final cut (see spreadsheet) but we selected the 30 Day Wilder’s Smoothing with End of Week Signals as the ultimate winner:
.

30 Day WS-MA, EWO Long .

Above you can see how the 30 Day WS-MA, EOW Long performed during the test period compared to the 75 Day EMA, EOW Long which was selected as the most effective Exponential Moving Average in a previous test. The WS-MA with this particular smoothing period produced almost identical results to the EMA but didn’t offer any benefits.

Upon further testing we found that despite very different calculation the WS-MA and the EMA are actually the same indicator. Simply double the WS-MA period and subtract one to find the equivalent EMA. For instance a 38 period WS-MA is identical to a 75 period EMA.

– The average annualized return of the 16 markets during the testing period was 6.32%. The data used for these tests is included in the results spreadsheet and more details about our methodology can be found here.

Exponential Moving Average (EMA)

The Exponential Moving Average (EMA) is a very popular method for smoothing data in an attempt to eliminate noise and our tests show that it is also highly effective. Unlike the Simple Moving Average (SMA) that applies equal weight to all data, the EMA applies more weight to the recent data so that it reacts faster to sudden changes.

You can see see why it is called an Exponential Moving Average when you look at how the weighting is applied; it is in the shape of an exponential curve. Because of this the weighting never reaches zero and the influence of early data always remains (although it has little effect outside of the specified smoothing period). This is more clearly illustrated by the chart below which shows the weighting for a 50 period EMA and a SMA:

Weighting - Exponential Moving Average and a SMA .

Although we call it a 50 period EMA, those 50 periods only actually account for 86% of the weighting. A further 12% is applied over the preceding 50 periods leaving the last 2% to be spread amongst all the prior data. Here is a great article from MarketSci on this topic: Visual Depiction of SMA vs EMA Weighting

How To Calculate an Exponential Moving Average

Calculating an Exponential Moving Average actually requires less processing power than a Simple Moving Average because it only refers to the current period and the previous EMA value. While it does not become active until the Nth period the EMA starts with the first close price and after that is calculated according to the following formula:

EMA = EMA(1) + α * (Close – EMA(1))

Where:

α = 2 / (N + 1)

N = The smoothing period.

Here is an example of a 3 period Exponential Moving Average:

How to Calculate an Exponential Moving Average

If you have two data sets and you wish to find out the EMA smoothing period, the following formula will reveal it:

N = (2-( (MA-MA[1]) / (Close-MA[1]) ) ) / ( (MA-MA[1]) / (Close-MA[1]) )

Exponential Moving Average Excel File

The EMA is so simple to calculate that it is unlikely that you would need a version in Excel but we have put together one for those of you that are lazy :). It is free and contains the ‘basic’ version you can see above and one that will automatically adjust to the length you specify. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Exponential Moving Average (EMA).

Exponential Moving Average and a Simple Moving Average

Exponential Moving Average vs Simple MA .

Test Results

If you haven’t already then check out the EMA test results. We tested it against the SMA and D-EMA through 300 years of data across 16 global markets to reveal which is the best and the characteristics they exhibit as their smoothing period is changed. See the results; Moving Averages – Simple vs Exponential

Linear Regression Indicator (LRI) & Time Series Forecast (TSF)

Linear Regression is a statistical tool used to predict future values from past values. By using the least squares method, a straight line can be plotted that minimizes the distance between the resulting line and the data set in order to reveal a trend.

The Linear Regression Indicator (LRI) plots the end value of a Linear Regression Line at each data point. A variation on the same idea is the Time Series forecast (TSF) which is found by adding the Linear Regression Slope to the Linear Regression Line. The TSF basically projects the LRI forward one period. The TSF is also sometimes referred to as a Moving Linear Regression or Regression Oscillator.

By calculating these two indicators on a moving basis the result looks similar to that of a moving average and can be used in the same way.

Calculating a Linear Regression Line

Linear Regression Line = a + bx

Where:

a = (Σy – bΣx) / n

b = (nΣ(xy) – (Σx) (Σy)) / (nΣx² – (Σx)²)

b = Linear Regression Slope.

x = The current time period.

y = The data series (Usually the close price).

n = Number of periods.

Linear Regression Indicator & Time Series Forecast Excel File

Calculating these indicators by hand is a pain in the ass so we have build an Excel spreadsheet containing both the Linear Regression Indicator and Time Series forecast that you can download for free. Find it at the following link near the bottom of the page under Downloads – Technical Indicators: Linear Regression Indicator (LRI) & Time Series Forecast (TSF). Please let us know if you find it useful.

Linear Regression Indicator, Time Series Forecast and a Simple Moving Average

Linear Regression Indicator, Time Series Forecast and SMA .

Test Results

We tested the Linear Regression Indicator and Time Series forecast through 300 years of data across 16 global markets to reveal which is the best and if either of them are worth using as trading tool for data smoothing – see the results.

Wilder’s Smoothing was developed buy J. Welles Wilder, Jr. and he used it as a component in several of his other indicators including the RSI which is one of the most popular technical indicators of all time.

Simple Moving Average (SMA)

The Simple Moving Average or SMA is probably the most commonly used technical indicator of all. It can be calculated by taking the average of a data series (usually the close price) over a set number of periods. As each period progresses the last value is dropped out of the calculation and the latest one takes its place; hence the ‘Moving’ characteristic.

Financial data is notorious for being full of noise. Smoothing methods like averages help to filter out some of that noise so that a clearer picture of what is really going on can be revealed. Test results show however the Simple Moving Average is certainly not the most effective smoothing method available. Why then do we use the SMA in the weekly ETF HQ Report?

Some Simple Moving Averages such as the 50, 100 and 200 day SMA are so widely followed that they regularly become important support and resistance levels. There is no reason why this should happen other than the fact that they have become a self fulfilling prophecy. If enough people think that a level is important then it becomes important:

200 Day Simple Moving Average as Support .

Above is an example the 200 day SMA acting as support and being seen as a buying opportunity for over a year. With so many points of inflection on this average the eventual break was viewed by traders as a significant technical failure and a flood of selling ensued.

For those of you who use Excel in your trading I have built a spreadsheet for you that contains a simple moving average. You are probably wondering why you would want to download such a simple indicator but this one is useful because it will automatically adjust to the length that you specify. We find this a useful feature and hopefully you will as well. Get the file at the following link near the bottom of the page under Downloads – Technical Indicators: Simple Moving Average (SMA). Please let us know if you find it useful.

Moving Average Test Results

Have you ever wondered which is better; a simple or exponential moving average? Well we tested both along with a double exponential moving average through 300 years of data across 16 global markets to reveal the answer. Here are the results – Simple vs. Exponential Moving Average

Weighted Moving Averages Put To The Test

A Weighted Moving Average smooths data by setting a separate but specific weighting for each data set over the length of its smoothing period. In this round of testing we will look at the standard Weighted Moving Average (W-MA), the Triangular Weighted Moving Average (TriW-MA) and the Sine Weighted Moving Average (SW-MA) in order to reveal which is the best and if any of them are worth including in your trading tool box.

To evaluate these averages we tested Long and Short trades using Daily and Weekly data, taking End Of Day (EOD) and End Of Week (EOW) signals with Moving Average lengths varying from from 5 – 300 days or 60 weeks.~ These tests were carried out over a total of 300 years of data across 16 different global indexes (details here).

Weighted Moving Average – Test Conclusion

Weighted Moving Average - Long and Short Annualized Return

Above you can see how the annualized return changes with the length of each Daily, EOD Moving Average for the Long and the Short side of the market. The relative performance of each MA was similar when going Long or Short but the returns on the Short side were much lower.

There is little difference in performance between the TriW-MA and the SW-MA while the W-MA was clearly superior. The W-MA performed particularly well with a setting of 35 days or 110 days, peaking with a annualized return of over 10% on these settings. As the smoothing period is extended beyond 110 days the returns gradually diminished.

Return to Top

Weighted Moving Average - Long and Short Annualized Return During Exposure

Above you can see the performance of each average during the time that it was exposed to the market. Across the board the efficiency of each average decreased as the length of each average is was increased. The W-MA again proved the most effective.

Return to Top

Best Weighted Moving Average – Long

We tested 357 averages on the Long side but rather than simply selecting the one with the greatest returns over the test period we looked for the following criteria:

Annualized Return > 9%
Average Trade Duration > 29 Days
Annualized Return During Exposure > 15%
Annualized Return on Nikkei 225 > 3%
Annualized Return on NASDAQ > 12.5%

8/357 Averages made the final cut (see spreadsheet) but we selected the 90 Day Weighted Moving Average with End of Week Signals as the ultimate winner:
.

90 Day W-MA, EOW Long

.
Above you can see how the 90 Day W-MA, EOW Long performed during the test period compared to the 75 Day EMA, EOW Long which was selected as the most effective Exponential Moving Average in a previous test. The Weighted MA produced very similar results to the EMA but didn’t offer any benefits.

Return to Top

Weighted Moving Average – Test Conclusion

The Triangular and Sine Weighted Moving Averages proved to be inferior to the W-MA while the standard Weighted Moving Average did produce reasonable returns. Those returns however, were similar (if slightly inferior) to those of an Exponential Moving Average while not offering any notable benefits. Therefore it can be concluded that none of the Weighted Moving Averages we tested are worth perusing further.

Return to Top