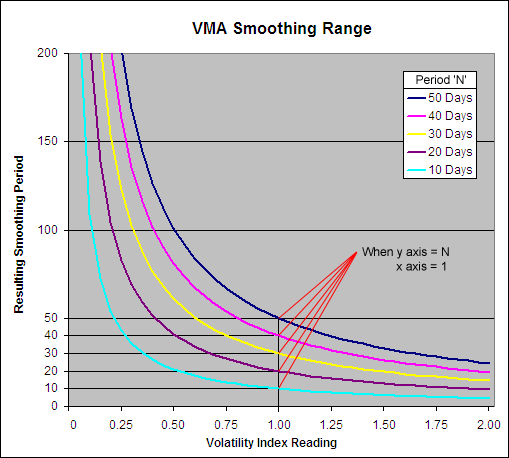
The Variable Moving Average (VMA) dynamically adjusts its own smoothing period to the changing market conditions based on a Volatility Index (VI). While any VI can be used, in this article we will look at how the VMA performs using a Standard Deviation Ratio (SDR). This is the VI that Tushar S. Chande first suggested be used when he presented what he called a Volatility Index Dynamic Average (VIDYA) in the March 1992 edition of Technical Analysis of Stocks & Commodities – Adapting Moving Averages To Market Volatility.
The SDR-VMA requires three user selected inputs: A Short Standard Deviation (SD1), a Longer Standard Deviation (SD2) and a VMA period. We tested trades going Long and Short, using Daily data, taking End Of Day (EOD) and End Of Week (EOW) signals~ analyzing all combinations of:
SD1 = 10, 20, 40, 80, 126
SD2 = 20, 40, 80, 126, 252
VMA = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
The SD lengths were selected due to the fact that they correspond with the approximate number of trading days in standard calendar periods: 10 days = 2 weeks, 20 days = 1 month, 40 days = 2 months, 80 days = ⅓ year, 126 days = ½ year and there are 252 trading days in an average year.
The VMA periods were selected after preliminary tests showed that when combined with the different SDR combinations, these settings resulted in a median smoothing period between 6 and 280 days; a range that should capture the best results based on what we know from previous research into moving averages.
A total of 390 different averages were tested and each one was run through 300 years of data across 16 different global indexes (details here).
Download A FREE Spreadsheet With Raw Data For
All 390 SDR-VMA Long and Short Test Results
.
SDR Variable Moving Average Test Results, Daily EOD, Long:
.
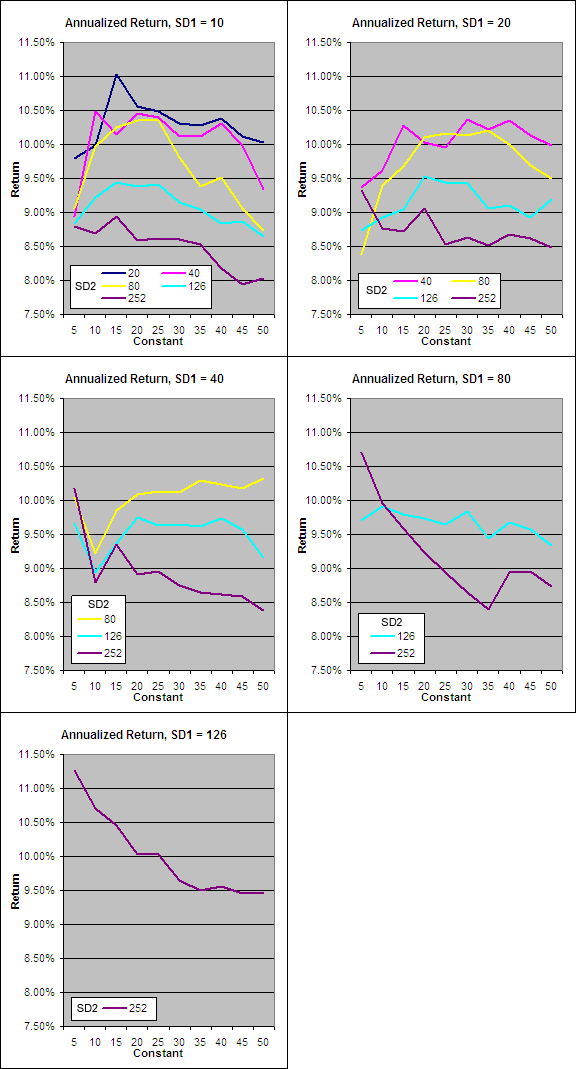
The data collected from our tests has been split by SD1 length with return plotted on the “y” axis, the VMA constant on the “x” axis and a separate series displayed for each SD2 length.
.
 .
.
First up it must be noted that every single SDR-VMA Long using EOD signals on Daily data outperformed the average buy and hold annualized return of 6.32%^ during the test period (before allowing for transaction costs and slippage). This is a vote of confidence for the concept especially seeing as each average was typically sitting in cash 37% of the time.
Perhaps the most interesting information from the data however is the fact that the best performer from each set had a SD2 that was twice the length of SD1. This formula of SD2 = 2*SD1 should therefore be used whenever utilizing the Standard Deviation Ratio.
.
The Best SDR-VMA Parameters
.
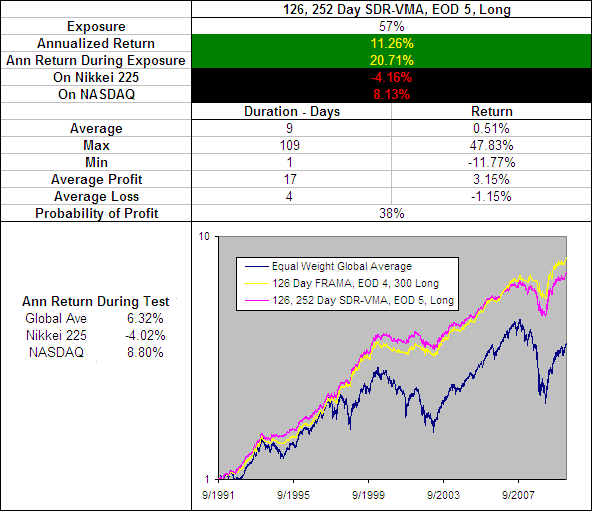
The best performing average was found where SD1 = 126, SD2 = 252 and the VMA constant = 5. In the FRAMA tests we also saw that the periods of 126 (half a year) and 252 (a full trading year) produced the best results so this appears to be a reoccurring theme:
.
 .
.
I have included on the above chart the performance of the 126 Day FRAMA, EOD 4, 300 Long becuase so far this has been the best performing Moving Average and as you can see the SDR-VMA under performs. To make matters worse it has an typical trade duration of just 9 days compared to the FRAMA’s 14, and underperformed the buy and hold returns of both the Nikkei 225 and the NASDAQ. Therefore we can conclude that the SDR-VMA, despite being effective is not as good as the FRAMA.
.
A look at the Smoothing Period:
.
 .
.
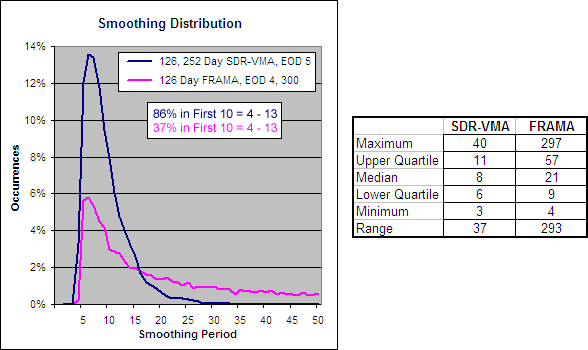
By looking at the smoothing distribution you can see why the SDR-VMA is so much faster than the FRAMA. While the FRAMA has a range of 293 days and a median of 21, the SDR-VMA has a range of just 37 days and a median of 8.
.
126, 252 Day SDR-VMA, 5 – Alpha Comparison
.
To get an idea of the readings that created these results we charted a section of the alpha for the 126, 252 Day SDR-VMA, 5 and compared it to the best performing FRAMA to see if there were any similarities that would reveal what makes a good volatility index:
.
 .
.
The alpha patterns are similar for both the 126 Day FRAMA 4, 300 and the 126, 252 Day SDR-VMA 5 but the readings are still very different. The SDR-VMA’s indicator is nearly always higher than the FRAMA’s which is why the resulting VMA is much faster.
It is desirable to see however that the SDR-VMA’s alpha is so clean and noise free in its movements. This leads me to believe that the 126, 252 SDR would be a good VI if it were adjusted to produce a slower average. Also due to the lack of noise from the SDR it may offer value in other applications such a way of ranking a universe of stocks by their trend strength, but that is the topic of another set of tests.
.
For more in this series see – Technical Indicator Fight for Supremacy
.
- ~ An entry signal to go long (or exit signal to cover a short) for each average tested was generated with a close above that average and an exit signal (or entry signal to go short) was generated on each close below that moving average. No interest was earned while in cash and no allowance has been made for transaction costs or slippage. Trades were tested using End Of Day (EOD) and End Of Week (EOW) signals on Daily data. Eg. Daily data with an EOW signal would require the Week to finish above a Daily Moving Average to open a long or close a short while Daily data with EOD signals would require the Daily price to close above a Daily Moving Average to open a long or close a short and vice versa.
- ^ This was the average annualized return of the 16 markets during the testing period. The data used for these tests is included in the results spreadsheet and more details about our methodology can be found here.