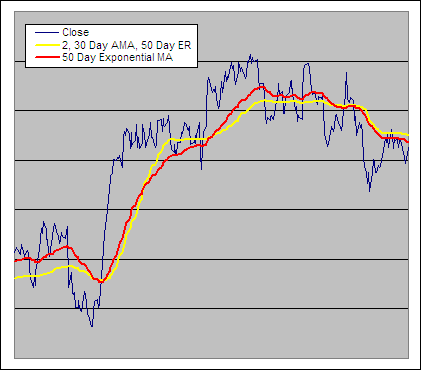
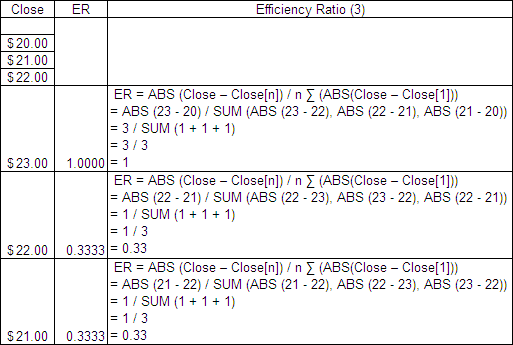
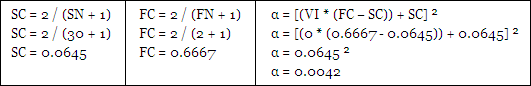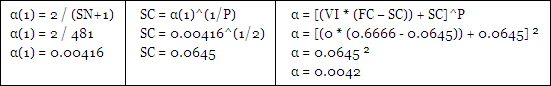The Adaptive Moving Average (AMA) modifies the amount of smoothing it applies to data in an attempt to adjust to the changing needs of a dynamic market. It makes these adjustments based on the readings from a Volatility Index (VI). Any measure of volatility or trend strength can be used, however in this article we will focus on how the AMA performs using the Vertical Horizontal Filter (VHF).
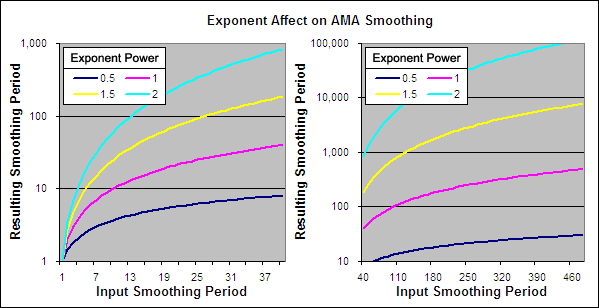
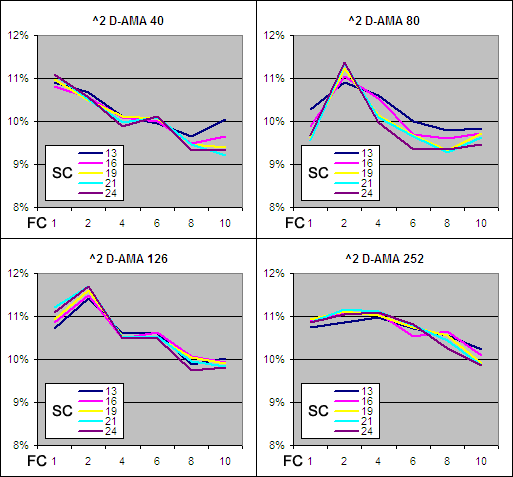
The VHF-AMA requires four user selected inputs: A Vertical Horizontal Filter period, a High – Low smoothing period range for the AMA and a power that Alpha is raised to. With four variables there are thousands of possible combinations so we had to make some educated assumptions based on our previous tests to narrow the choices down.
In our tests on the Vertical Horizontal Filter in a VHF-VMA we revealed that VHF periods of 126, 252 and 80 produced the best results. Because Volatility Index settings have proven to produce similar results in both the VMA and the AMA, testing these three settings should be sufficient to capture the best results. Also they corresponded with the approximate number of trading days in standard calendar periods: 80 days = ⅓ year, 126 days = ½ year and there are 252 trading days in an average year, so:
VHF = 80, 126, 252
In previous tests we have seen that a moving average range produces the best results when it can move to as little as 4 periods or less, therefore we will test:
AMA Actual Fast Moving Average (FN) = 1, 4, 10
With the slow moving average we have consistently seen 300 produce the best results while changing this setting hasn’t usually made a big impact. However we still ran tests through several settings:
AMA Actual Slow Moving Average (SN) = 200, 250, 300
For the Alpha Power we also tried several variables:
Alpha Power (P) = 0.5, 0.75, 1, 1.5, 2, 2.5
We tested trades going Long, using Daily data, taking End Of Day (EOD) signals~ analyzing all combinations of the above settings.
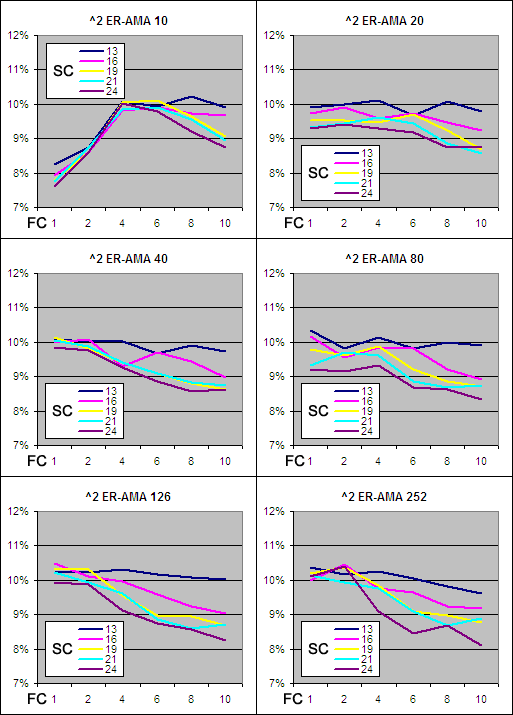
Each time the Alpha Power was adjusted the SC and FC had to be modified to account for the change but the actual FN and SN stayed the same.
For instance a SC – FC range of 1 – 24 with alpha ^ 2 has an actual FN – SN range of about 1 – 300 due to the effect of squaring alpha. Here is a table that shows the SC – FC ranges used so that the FN – SN ranges stayed constant regardless of ‘P’:

If that doesn’t make a lot of sense then please read our explanation of the Adaptive Moving Average. A total of 162 different averages were tested and each one was run through 300 years of data across 16 different global indexes (details here).
Download A FREE Spreadsheet With Raw Data For
Vertical Horizontal Filter Adaptive Moving Average – Test Array
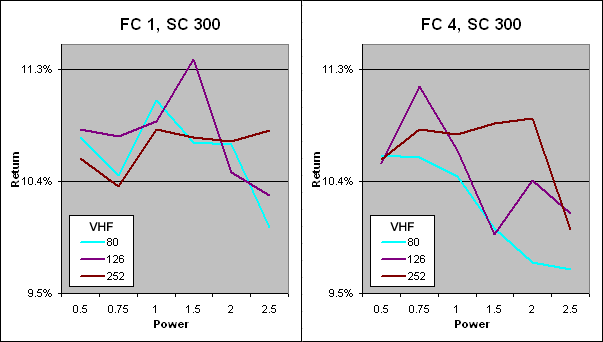
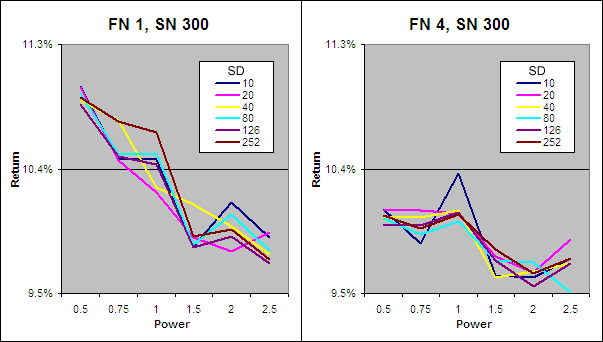
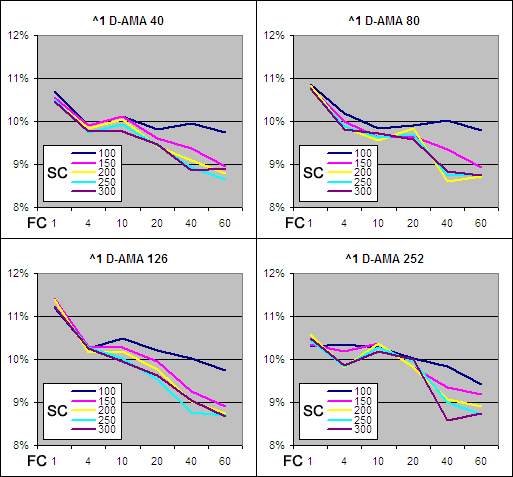
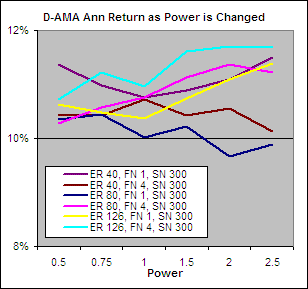
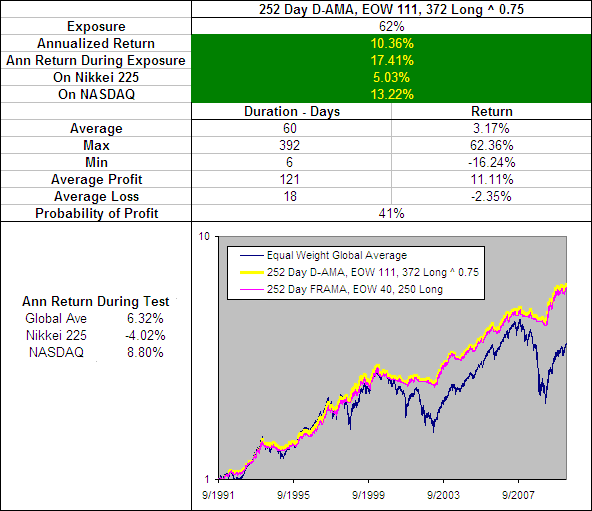
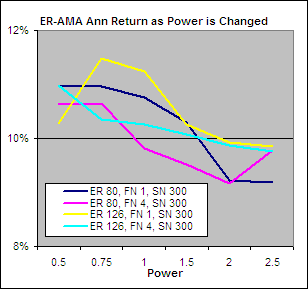
Above we have charted the annualized returns achieved from each VHF with Alpha raised to different powers along the X axis. The chart on the left shows the results when the FN = 1 and SN = 300 while on the right FN = 4 and SN = 300. Clearly keeping the FN at 1 is important to achieve the best returns. A VHF period of 126 stood out as the best performer and this echoes previous tests. Finally, when FN = 1, raising Alpha to the power of 1.5 yielded the best results.
Best Vertical Horizontal Filter Adaptive Moving Average
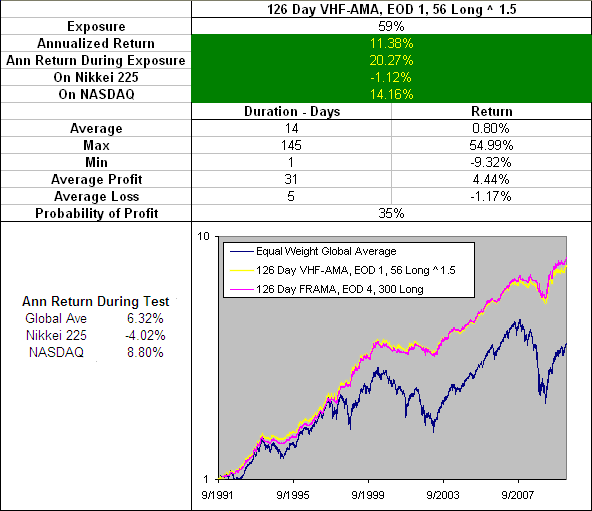
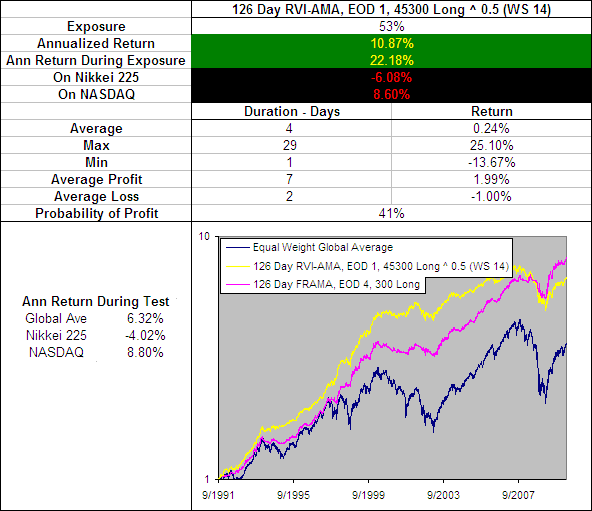
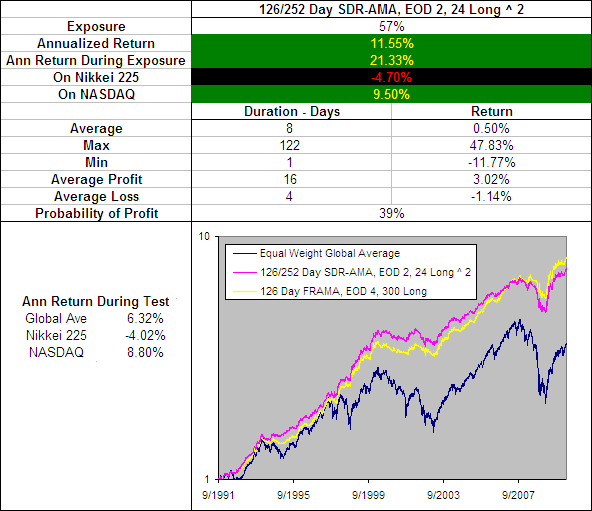
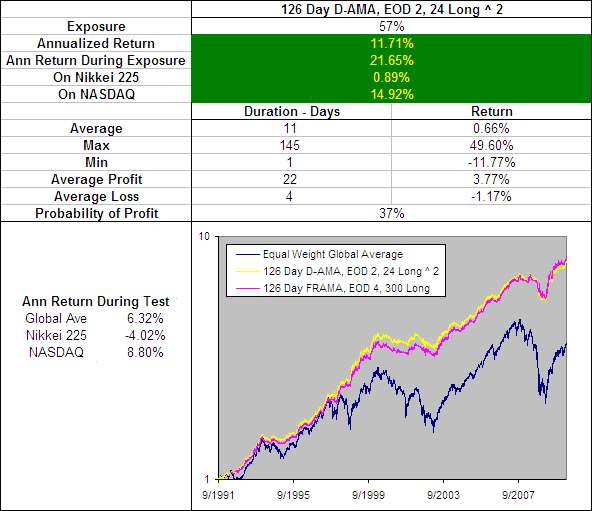
Included on the above chart is the performance of the 126 Day FRAMA, EOD 4, 300 Long because so far this has been the best performing Moving Average. The 126 Day VHF-AMA, EOD 1, 56 Long ^ 1.5 produced extremely similar results and even had the same average trade duration of 14 days. However it did slightly underperform the FRAMA by most measures but lets take a quick look under the hood to see what makes it tick:
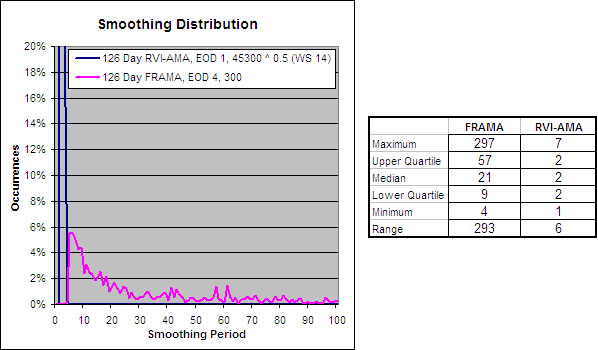
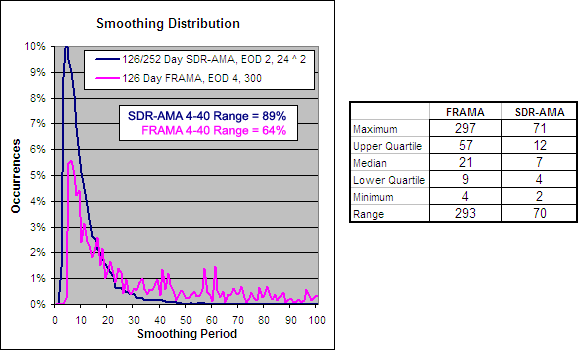
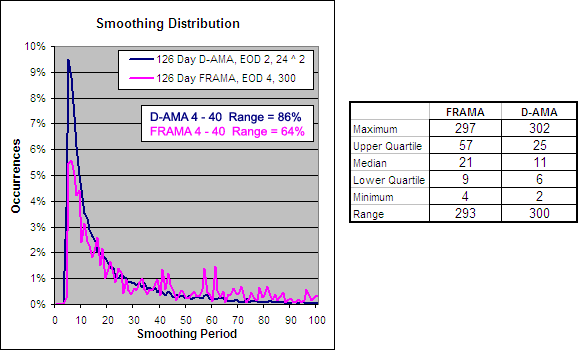
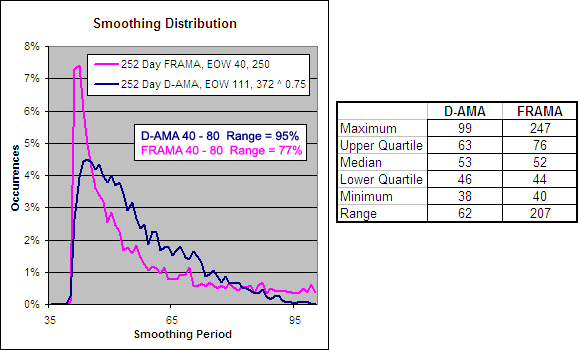
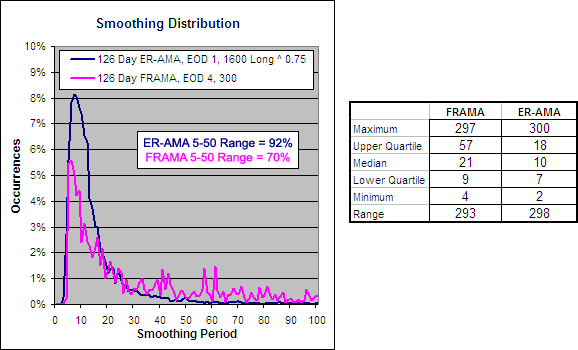
126 Day VHF-AMA, EOD 1, 56 ^ 1.5 – Smoothing Period Distribution

As you can see the VHF-AMA does not have nearly as much of a spread with its smoothing range as the FRAMA. A larger range makes the FRAMA more able to adapt to different market environments.
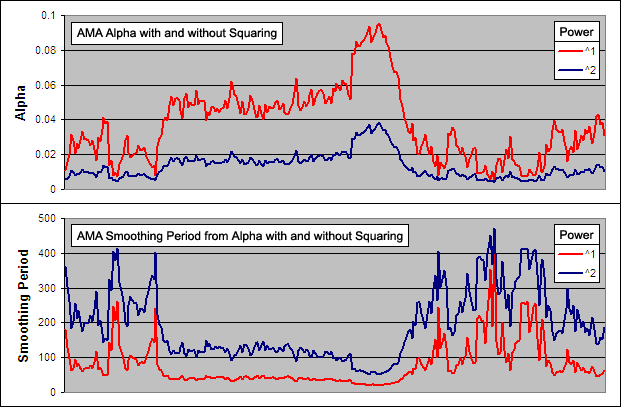
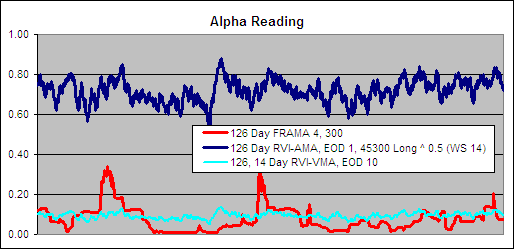
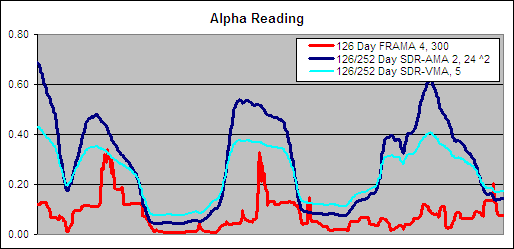
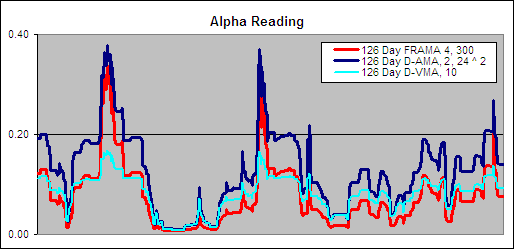
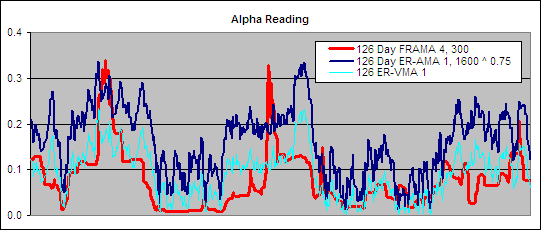
126 Day VHF-AMA 1, 56 ^ 1.5 – Alpha Comparison
To get an idea of the readings that created these results we charted a section of the alpha for the 126 Day VHF-AMA 1, 56 ^ 1.5 and compared it to the best performing FRAMA and the best VHF-VMA to see if we could learn what makes a good volatility index for use in an AMA:.

The VHF does not look as though it can change as nimbly as the FRAMA while both the AMA and VMA using a VHF look very similar.
Excel Spreadsheet
The VHF is outstanding for use in an AMA and we have build an excel spreadsheet for you to download free so you can have a play. Simply use the flowing link and you will find it under Downloads – Technical Indicators: Adaptive Moving Average (AMA).
For more in this series see – Technical Indicator Fight for Supremacy
- ~ An entry signal to go long for each average tested was generated with a close above that average and an exit signal was generated on each close below that moving average. No interest was earned while in cash and no allowance has been made for transaction costs or slippage. Trades were tested using End Of Day (EOD) signals on Daily data. Eg. Daily data with EOD signals would require the Daily price to close above a Daily Moving Average to open a long and to close below that Average to close the position.
- We used the average annualized return of the 16 markets during the testing period. The data used for these tests is included in the results spreadsheet and more details about our methodology can be found here.



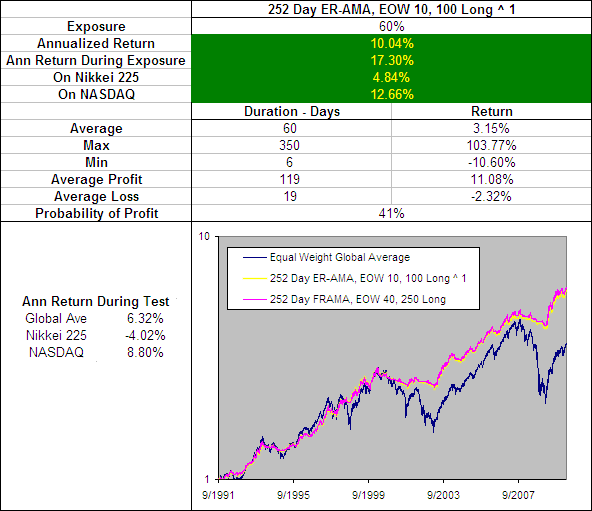
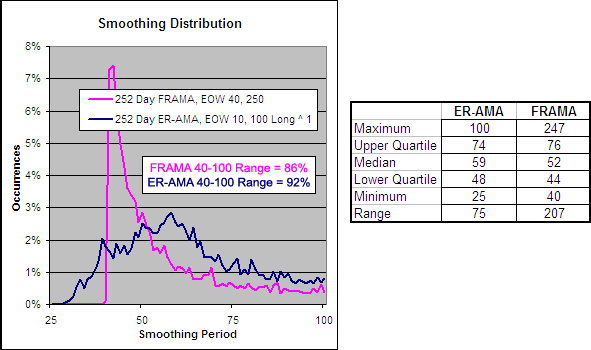
 We have included on this chart the best EOW FRAMA and EOW ER-VMA. The ER-VMA and ER-AMA use the same volatility index but the 252 Day ER-AMA 10, 100 ^1 results in a higher Alpha which explains the faster average. The Alpha for the FRAMA and the AMA does stay in a similar zone but the FRAMA is far less volatile which is preferable.
We have included on this chart the best EOW FRAMA and EOW ER-VMA. The ER-VMA and ER-AMA use the same volatility index but the 252 Day ER-AMA 10, 100 ^1 results in a higher Alpha which explains the faster average. The Alpha for the FRAMA and the AMA does stay in a similar zone but the FRAMA is far less volatile which is preferable.